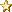Konverteringsformel for sensitivitet oppgitt som dB/V og dB/mW hentet fra Head-Fi.org-tråden "dB per milliWHAT? Efficiency vs. Sensitivity vs. "How loud do they really go?"" (min uthevning).En liten digresjon; noen som vet forholdet mellom SPL/V og SPL/mW?
I ovensiterte innlegg referer aabottom til et eksempel med Sennheiser HD 650 hentet fra nevnte innlegg #37:post #19 of 25 2/25/10
Convert sensitivity in dB/V to sensitivity in dB/mW.
- aabottom
- 40 Posts. Joined 2/2010
- Location: MD
Another good sensitivity thread.
[...]
I just replied to a thread (see post #37) where I put "an actual conversion formula" to convert sensitivity in dB/V and impedance to sensitivity in dB/mW.
The formual gets the same results as post #18 above. I'll repeat the equation here for reference.
==== Extra Credit =============
For the geeks out there, the equation to convert dB/V to dB/mW is
dB/mW = dB/V + 10*log(R*P/V^2)
where
dB/V is the sensitivity in dB (SPL) at 1 Vrms of voltage into impedance R, 103 dB/V into 300 ohms in this case
R is the nominal impedance, 300 ohms in this case
V is the reference voltage, 1 Vrms in this case
P is the reference power, 0.001 watt in this case
dB/mW is the sensitivity in dB (SPL) at 0.001 watt of power (that is 1 milliwatt)
log is the logarithm base 10
In the above example we have:
dB/mW = 103+10*log(300*0.001/1^2) = 98.7
post #37 of 38 2/25/10
[...]
For example, on their website, Sennheiser gives the following specifications for their HD 650:
Nominal impedance: 300 ohms
Sound pressure level (SPL): 103 dB (1 Vrms).
[...]
Sist redigert: