Begrepsordliste

Begrepsforvirring er utbredt i hifi-debatten, her er noen grunnleggende som kan være nyttig å holde styr på. Hensikten er å gi en lettfattelig, ikke-matematisk "magefølelse" for hva de ulike begrepene betyr. Mer formelle forklaringer vil henvises til med linker til aktuelt materiell.

dB: DeciBel. Én tidels Bel. Logaritmisk måleenhet for amplitude eller effekt opp mot en referanse.
I tilfellet effekt: dBout=10*log(Pout/Pref).
I tilfelle amplitude: dBout=20*log(Aout/Aref)
I akustikk: Lydtrykk relativt til referanseverdien 20µPa (0dB). SPLdB=20*log(P/20µPa).

SNR: Signal-to-Noise-Ratio. Forholdet i dB mellom signaleffekt og integrert støyeffekt i det aktuelle frekvensbåndet (for audio, typisk 20hz-20khz).

SNDR: Signal-to-Noise-and-Distortion-Ratio. Som SNR, men også inklusive harmonisk forvrenging.

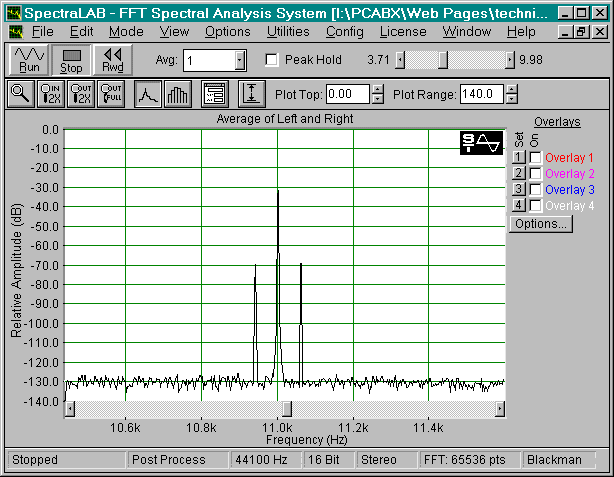
SFDR: Spurious-Free-Dynamic-Range. Samme som dynamisk område. Avstanden i dB mellom maks signalamplitude og høyeste forvrengingskomponent.

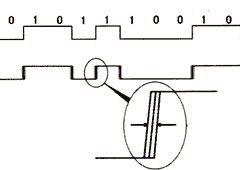
Binære tall: Tallrepresentasjon modulo-2, eller med andre ord: 0 (0), 1 (1), 10 (2), 11 (3), 100 (4), 101 (5) osv.

Bit: Binært siffer.

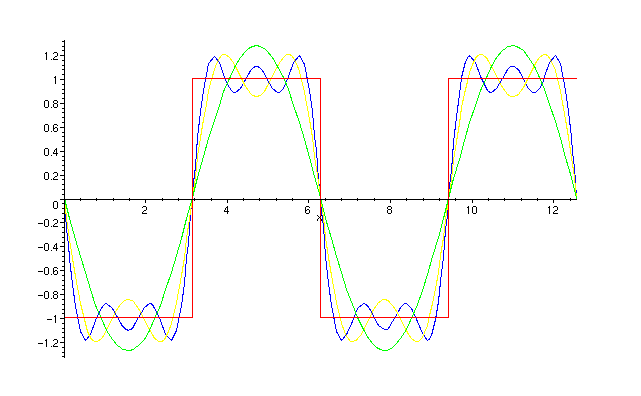
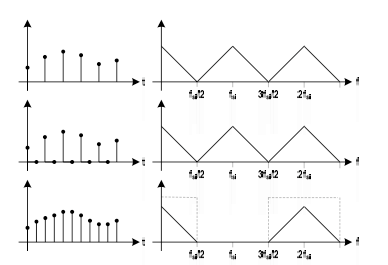
Sampling: Å representere et tidskontinuerlig signal som en rekke punktprøver (sampler) tatt med en gitt frekvens (samplingsfrekvensen). Det kan vises at sampling er en tapsfri prosess for alle signaler opp til halve samplingsfrekvensen (Nyquist-frekvensen). Over halve samplingsfrekvensen er prosessen destruktiv, dvs ingen informasjon kan bevares. For matematisk bevisførsel, se aktuell Wikipedia-artikkel (under "proof"),

Aliasing: Hvis man prøver å sample et signal over nyquist-frekvensen, vil dette føre til et uønsket alias like langt under nyquist-frekvensen som det opprinnelige signalet var over. Man sier at signaler som samples foldes rundt nyquist-frekvensen. For å unngå uønsket aliasing ved sampling, må alt signalinnhold over nyquist-frekvensen filtreres vekk først (kalt antialiasing eller antialias-filter).

Kvantisering: Å tilordne et amplitudekontinuerlig signal diskrete verdier (skalar kvantisering) eller vektorer (vektorkvantisering). Hvis dette er verdier med lik avstand kalles kvantiseringen uniform skalar kvantisering. Utgangsverdien representeres som oftest binært. En kvantisering til heltall mellom 0 og 2B kan representeres med B bit.
Det kan vises at for B-bit uniform skalar kvantisering, vil feilen bli en hvitstøy med nivå ca 6*B dB under maksimalt signalnivå (Bennett's quantization noise model). En B-bit kvantiserer har følgelig 6*B dB SNR. Bennetts støymodell er kun en tilnærming, for mer detaljerte modeller se publikasjoner av Bernard Widrow, Lipshitz/Vanderkooy m.fl..

Dither: En prosess for å "tvinge" kvantiseringen til å overholde Bennett's støymodell. Hvis et egnet støysignal summeres til inngangssignalet før kvantisering, vil kvantiseringsprosessen kun resultere i hvit støy og ikke forvrenging.

Digitalisering: Hvis et signal samples og så kvantiseres har det en definert datamengde (B bit, se "kvantisering") som inntreffer med et gitt intervall (samplingsfrekvensen, se "sampling"). Følgelig har det en gitt bitrate (bps = bit pr. sekund) og kan lagres digitalt. Bitraten vil være gitt av BPS=B*fs hvor B er ordbredden og fs er samplingsfrekvensen.

ENOB: Effective Number of Bits. Et signal kvantisert til B antall bit har en SNR gitt av 6*B (se "kvantisering"). Følgelig har enhver prosess, analog eller digital, med en gitt SNR, samme dynamiske område som et signal kvantisert med SNR/6 bit. Dette er prosessens ENOB.

Fortsettes...

Dempingsfaktor: En forsterkers utgangsimpedans normalisert til en gitt last, som oftest 8ohm. Ergo; har forsterkeren dempingsfaktor 100 er utgangsimpedansen 8ohm/100 = 0.08ohm.

Frekvens: Et mål på hvor ofte en gjentagende, stasjonær hendelse skjer pr tidsenhet, som oftest ett sekund (i hvis tilfelle frekvensen måles i 1/s=Hz). Akustiske bølger som gjentar seg mellom 20 og 20.000 ganger pr sekund oppfattes som lyd. Det inverse av frekvensen, altså hvor lang tid det går mellom hver gang hendelsen gjentar seg, kalles periodetiden.

Fase: Tidsforskjell normalisert til periodetid. Hvis to periodiske signaler med samme frekvens, feks 400hz, er forskjøvet i tid i forhold til hverandre, feks 0.001sek, er faseforskyvningen mellom de to 0.001sek*400hz*360grader=144 grader. Fase er en relativ størrelse som ikke har noen mening uten en referanse å sammenligne den med. Når en impedans sies å ha en gitt fase ved en frekvens, betyr det hvor mye strømmen gjennom den vil forsinkes med referanse til påtrykt spenning ved denne frekvensen.

Bølgelengde: Lengden på en bølge, - akustisk, elektromagnetisk eller annet. Lyd beveger seg i luft med en hastighet på 340m/s, hvilket gjør at bølgelengden blir 340/f hvor f er frekvensen. Elektromagnetiske bølger i ledere beveger seg med tilnærmet lyshastigheten, 300.000.000m/s, hvilket gjør at bølgelengden blir 300.000.000/f, hvor f er frekvensen. For 20kHz, høyeste audiofrekvens, er den akustiske bølgelengden 1.7cm (som betyr at faseforskyvingen er 360 grader pr 1.7cm). For elektriske signaler i ledere er den samme ca 15 kilometer.

Kapasitans: Mengden statisk ladning som lagres mellom to ledere med en gitt spenningsdifferanse. Kapasitansen øker med arealet de har mot hverandre, avtar med avstand de har fra hverandre og avhenger av ladningsegenskapene, permittiviteten, til isolasjonen (dielektrikumet) mellom dem. Kapasitans mellom to ledere er ofte uønsket, i hvis tilfelle det omtales som parasittisk kapasitans. Dersom lagring av statisk ladning er ønsket, bruker man to ledere med stort areal som ligger tett inntil hverandre og et dielektrikum som gir høy kapasitans imellom. Dette kalles en kondensator. AC-signaler vil lekke gjennom en kapasitiv kobling. En kapasitans AC-motstand er gitt av 1/(2*pi*f*C) hvor C er kapasitansen og f er frekvensen. For mer om kondensatorens kretstekniske oppførsel, se aktuell Wikipedia-artikkel.

Induktans: Et mål på hvor mye magnetisk fluks en leder setter opp når det går en gitt strøm gjennom den. Induktansen avhenger av lederens geometri samt magnetiseringsevnen, permeabiliteten, til materialet omkring den. Hvis induktans er ønskelig vikler man gjerne lederen i en spoleform rundt et kjernemateriale med høy permeabilitet. Induktans vil fungere som en motstand for AC-signaler som øker med frekvens. Den er gitt av 2*pi*f*L, hvor f er frekvensen og L er induktansen. For mer om induktorers kretstekniske oppførsel, se aktuell Wikipedia-artikkel.

Forvrenging: Enhver endring eller deformarsjon av et signal betegnes som forvrenging eller distorsjon. Ethvert periodisk signal kan rekkeutvikles til en uendelig sum sinusbølger (for mer info se Wikipedia: Fourier-rekker), det vil si x(t)=a1*sin(ft)+a2*sin(2ft)+a3*sin(3ft)..... hvor f er grunnfrekvensen til signalet og a2, a3 osv er de harmoniske komponenter. En deformasjon av et periodisk signal vil føre til en endring av det harmoniske innholdet og kalles harmonisk forvrenging.


Figur 1: Hvordan et periodisk signal, her en firkantbølge, består av harmoniske komponenter. Grønn = a1, gul = a1+a3, blå = a1+a3+a5, rød = a1+.....+ainf. For en firkant kan det vises at a2=a4... = 0. De like harmoniske gir asymmetri, de odde gir symmetri og firkantpulsen er helt symmetrisk.

THD: Total Harmonisk Distorsjon. Et mål på den totale harmoniske forvrenging i prosent av signalets effekt. I praksis måles harmonisk forvrenging normalt på en ren sinus, som opprinnelig kun inneholder leddet a1. Effekten til alle komponenter fra a2 og oppover vil da utgjøre THD. I praksis begrenser man beregningen til de 6-8 laveste harmoniske komponenter. I en forsterker vil deformasjonen domineres av komprimering nær maksnivå, som gir 3.harmonisk i en symmetrisk (push-pull) og 2.harmonisk i en asymmetrisk (single-end) kobling.

Linearitet: Den formelle definisjonen på linearitet er at en funksjon overholder følgende to egenskaper: 1) f(x + y) = f(x) + f. 2) f(ax) = af(x) for alle a. Det betyr i praksis at en lineær prosess kun vil skalere et inngangssignal opp eller ned. Signalets harmoniske sammensetning vil ikke endres (se egenskap 1 og fourierrekken). To signaler som blandes vil heller ikke i en lineær prosess modulere hverandre (egenskap 2).

Skin-effekt: Skin-effekt er et bølgefenomen i ledere som skyldes elektromagnetisk (selv)induksjon. Et elektrisk felt følges av et magnetisk felt som er transverst på det selv. Ved høye frekvenser vil det magnetiske feltet motinduserte strømmer som fører til reduksjon av netto strømtetthet i sentrum av lederen. Jo høyere frekvenser, jo mer motinduksjon og strømtransporten vil i større og større grad kun kunne gå i overflaten. Dette gjør at resistansen i en leder øker ved høye frekvenser siden det effektive tverrsnittet avtar. Skindybden er en betegnelse på hvor langt fra overflaten strømtettheten er redusert med en faktor e (naturlig logaritme) ved den gitte frekvensen. Jo mer magnetiserbart ledermaterialet er (høyere selvinduksjon), jo mindre er skindybden og den reduseres proposjonalt med kvadratroten av frekvensen.

For kobber og så lave frekvenser som audio (under 50kHz) er skindybden så stor at man ikke får signifikant resistansøkning med mindre lederen er mange titalle eller hundretalls kvadratmillimeter i tverrsnitt, og i så tilfelle er den (resistansen) så forsvinnende liten i utgangspunktet at det knappest er et praktisk problem (det største praktiske problemet med fem hundre kvadratmillimeters kabel ville trolig heller gått på terminering). Men over en viss tykkelse vil du ved høye frekvenser ikke lengre få bedre ledningsevne ved å bytte til enda tykkere kabel. For formler til å kunne beregne effektiv resistans og skindybde, se Wikipedia: Skin-effect.

Proximity-effekt: Proximity-effekt er i prinsippet det samme fenomenet som skin-effekt, men nå som konsekvens av gjensidig motinduksjon i to ledere som ligger inntil hverandre. Dette vil også føre til en økning av resistansen ved høye frekvenser, men igjen er det et fenomen som først vil få noen effekt langt over audioområdet (MHz-området og oppover).

Tusen takk, hr Løkken. (dette er faktisk ikke spydig)

Kunne du kanskje skrevet en begrepsordliste for dummies, rettere sagt en ordliste tilpasset meg ;D

Lin

Noe sånt?

Høyttaler: Enhet som omsetter elektrisk spenning til lyd. Kan koste flere hundre tusen kroner. Bedømmes kvalitativt etter følgende premiss: Jo større, tyngre og styggere, jo bedre (også kalt "telefonkioskfaktor").

Edit: Jeg tar det vel for gitt at potensielle lesere av "tech-hjørnet" allerede er temmelig fortapte sjeler, - en ordliste for normale, sinnsfriske mennesker, en slags "innfallsport til hifi-sjargongen", er slett ingen dum idé.

Proximity-effekt: Proximity-effekt er i prinsippet det samme fenomenet som skin-effekt, men nå som konsekvens av gjensidig motinduksjon i to ledere som ligger inntil hverandre. Dette vil også føre til en økning av resistansen ved høye frekvenser, men igjen er det et fenomen som først vil få noen effekt langt over audioområdet (MHz-området og oppover).

Klikk for å utvide...

Vil bare legge til at proximity effect er et begrep man bruker innen mikrofonteknikk og, og da om kardioide- og åttetallsmikrofoners hang til å gi en markant basshevning i signalet når kilden står veldig nær mikrofonen. Veldig merkbart i en del radiosendninger og ikke minst i danske TV-reklamer.

Legg til alt du vil, - hadde i utgangspunktet ikke tenkt å gjøre dette alene...

telefonkioskfaktor, den var morsom.

Noe sånt?

Høyttaler: Enhet som omsetter elektrisk spenning til lyd. Kan koste flere hundre tusen kroner. Bedømmes kvalitativt etter følgende premiss: Jo større, tyngre og styggere, jo bedre (også kalt "telefonkioskfaktor").

Klikk for å utvide...

Jepp ;D

telefonkioskfaktor, den var morsom.

Klikk for å utvide...

Det er få som vet det, men jeg er faktisk 7% morsommere enn gjennomsnittet.

Da er du kanskje faktisk hele 56% av en luring også da?

Alltid like gøy for eksempel å høre i en reklame at det nye lurium x smaker 34% bedre enn den gamle varianten.

Jitter: Jitter betyr usikkerhet/nervøsitet eller fysisk skjelving. I digtial signalbehandling brukes jitter som et begrep på tidsmessig avvik i transisjonene til digitale data relativt til den ideelle samplingsperioden. Avvik i sampleperioden i overgangen fra diskret til kontinuerlig tid eller vice versa (dvs. DA eller AD-konvertering) vil medføre en forvrenging av signalet, eller økt støy hvis jitteret ikke er signalkorrelert.


Jitter i en digital signalstrøm

Samplingsinstanten i et digitalt signalsystem er definert av en separat klokke og denne er hovedkilden til samplingsjitter. Tidsavviket i klokken er ofte en kombinasjon av:

1) Ukorrelert, tidsmessig støy; som følge av begrenset nøyaktighet og elektrisk støy som man finner i alle kretser.
2) Sinusoide avvik; som følge av at frekvensen til klokkegeneratoren ofte moduleres av rippel på forsyningsspenningen og dennes harmoniske.
3) Signalavhengige avvik; som følge av at klokke og signal i noen deler av digitale audiosystemer, feks S/P-DIF-overføringer, multiplekses og overføres på samme leder.

Sinusoid jitter, signalmodulert såvel som forsyningsmodulert, vil medføre forvrenging som oppstår som sidebånd til det opprinnelige signalet. For en vanlig PCM DAC eller ADC vil forvrengingen tilnærmet være gitt av:

Rj=20*log(J*2*pi*fsig/4)

Der J er jitteramplituden i sekunder, fsig er signalfrekvensen i Hz og Rj er nivået på den resulterende forvrenigngskomponenten i dB relativt til signalnivået. Forvrengingskomponenten vil oppstå ved fsig+/-fjit der fjit er frekvensen til jitterkomponenten.


Forvrengingskomponenter som følge av jitter

Støyaktig jitter vil føre til en generell heving av støygulvet til AD- eller DA-konverteren. Beregning av det resulterende støynivået er noe mer komplisert, men generelt for de jitternivåer man finner i gode CD-spillere er bidraget -110dB relativt til fullt signalnivå eller lavere.

1-bit DA- eller AD-konvertere vil generelt gi et betydelig høyere forvrengingsnivå for en gitt mengde jitter enn multibit ditto.

En jitterdemonstrasjon kan lastes ned her. Som det kan ses er jitternivået på testsporene hhv. -20dB, -40dB, -60dB og -80dB. Til sammenligning er jitternivået i en moderne, god CD-spiller ca -120dB (hundre ganger lavere enn det laveste testnivået).

Du mener vel ganger og ikke grader løkken?

Fint forklart. Hadde bare alle som argumenterer med jitter leste dette...

-k

Korrigert, takker.

Oversampling: Prosess for å øke samplingsfrekvensen med et heltall antall ganger. Prosessen består av to trinn. Det første er såkalt zero-stuffing. For en oversampling med faktor L, vil L-1 nullsampler settes inn mellom de eksisterende. Man vil da ha uendret frekvensinnhold, med andre ord er alle alias over den gamle sampleraten fortsatt tilstede, nå i det nye basebåndet. Disse fjernes ved å lavpassfiltrere eller interpolere. Med et ideelt interpolasjonsfilter vil alle alias fjernes, med andre ord vil kun den opprinnelige signalkomponenten være til stede i det nye basebåndet og prosessen er tapsfri. Aliasing skjer nå kun ved multiplum av den nye, mye høyere sampleraten. Dette tillater mye enklere analoge rekonstruksjonsfilter på utgangen av den DACen, eventuelt antialiasfilter på inngangen av ADCen. Alle moderne ADCer og DACer er oversamplet, normalt mellom 64 og 256 ganger. Oversampling kan ytterligere begunstige ADC og DAC design, siden man kan redusere antall bit kraftig og ved hjelp av støyforming flytte den resulterende kvantiseringsstøyen høyt opp i frekvens siden nyquistbåndet nå er stort i forhold til det hørbare frekvensområdet. Slik kan man realisere en DAC eller ADC med svært få, eller bare én, bit og allikevel bevare høy oppløsning i audioområdet. Denne prosessen kalles delta-sigma modulasjon og brukes i praktisk talt alle ADCer og DACer. Det må bemerkes at støyforming aldri øker oppløsningen til kilden, kun til bitreduksjonen i selve støyformeren. For delta-sigma modulatoren opptrer støy fra kilden som en del av inngangssignalet og kan ikke fjernes. Med andre ord kan en 1-bit delta-sigma DAC med 16-bit inngang, oppnå maks 16 bit effektiv oppløsning. Oversampling er illustrert i tidsdomenet og frekvensdomenet i figuren under for en faktor L=2. Ideelt sett (les: med ideelt lavpassfilter) er oversampling en tapsfri prosess, i realiteten vil filteret være ikke-ideelt og man vil kunne få en liten mengde aliasing i basebåndet.



Upsampling: En prosess teknisk sett nært relatert til oversampling, men hvor sampleraten økes med en faktor som ikke er heltall, feks fra 44.1kHz til 96kHz. Dette gjøres ved at man først oversampler kraftig, deretter nedsampler igjen. Hvis man skal upsample fra 44.1kHz til 96kHz, en faktor på 320/147, må man først oversample med en faktor 320, så nedsample med en faktor 147. Prosessen forøvrig er den samme som beskrevet for oversampling. Man kan også ha varierende samplerateendring, med en annen klokkekilde på utgangen enn inngangen, hvorpå faktoren justeres kontinuerlig ved hjelp av en såkalt frekvenssporer (frequency tracker) som kontinuerlig sporer frekvensforholdet mellom utklokken og innklokken. Hensikten med upsampling er som oftest å kunne koble ulike kilder med ulik samplerate (feks CD og DVD), eventuelt også med ulike klokkekilder, til samme DAC. I likhet med oversampling, er upsampling ideelt sett en tapsfri prosess, men vil i praksis kunne medføre små menger alias-forvrenging. Hverken oversampling eller upsampling kan øke informasjonsinnholdet eller oppløsningen til kilden.

Betyr dette at synkron upsampling er det samme som oversampling?

Det blir et definisjonsspørsmål, normalt bruker man betegnelsen oversampling når konverteringsraten er heltall, oppsampling når den er fraksjonell.

Kan du forklare meg hva et differanseprodukt er?

Har nemlig aldri fått noen tilfredsstillende forklaring på det, til tross for at jeg vet at to frekvenser kan danne et differanseprodukt i et lavere toneleie.

Intermodulasjon: Hvis du kjører et signal med en 18kHz-komponent og en 19kHz-komponent gjennom en ulineær operasjon, vil du få et sumprodukt på 37kHz og et differanseprodukt på 1kHz. Disse kalles andre ordens intermodulasjonsprodukter. Du vil også få høyere ordens intermodulasjonsprodukter (tredje, fjerde osv) mellom alle mulige summer og differanser av de harmoniske til de nevnte komponentene. Figuren under viser andre og tredjeordens intermodulasjon, dvs slik spektrumet vil se ut hvis den ulineære operasjonen kun har andreharmonisk og tredjeharmonisk forvrenging. Total intermodulasjonsforvrenging kalles ofte IMD (intermodulasjons-distorsjon).

Mengden andreordens IMD vil være proporsjonal med mengden andreharmonisk, mengden tredjeordens IMD proporsjonal med mengden tredjeharmonisk osv. Hvis forsterkeren har lite THD har den derfor også lite IMD, de er begge resultater av ulinearitet.

Et strålende initiativ, perfekt for de av oss som kan for lite og ønsker presis informasjon istedenfor synsing.
HC

Ivar, i tråden om Hegel v.s. Krell dukker begrepet Dynamisk dempningsfaktor opp. Kan du kaste lys for en som vandrer i mørket?

Intermodulasjon: Hvis du kjører et signal med en 18kHz-komponent og en 19kHz-komponent gjennom en ulineær operasjon, vil du få et sumprodukt på 37kHz og et differanseprodukt på 1kHz. Disse kalles andre ordens intermodulasjonsprodukter. Du vil også få høyere ordens intermodulasjonsprodukter (tredje, fjerde osv) mellom alle mulige summer og differanser av de harmoniske til de nevnte komponentene. Figuren under viser andre og tredjeordens intermodulasjon, dvs slik spektrumet vil se ut hvis den ulineære operasjonen kun har andreharmonisk og tredjeharmonisk forvrenging. Total intermodulasjonsforvrenging kalles ofte IMD (intermodulasjons-distorsjon).

Mengden andreordens IMD vil være proporsjonal med mengden andreharmonisk, mengden tredjeordens IMD proporsjonal med mengden tredjeharmonisk osv. Hvis forsterkeren har lite THD har den derfor også lite IMD, de er begge resultater av ulinearitet.

Klikk for å utvide...

Kanskje et inngangs/utgangs-amplitude plot hadde vært til hjelp? Jeg tenker på noe ala http://ccrma.stanford.edu/~jos/pasp/Nonlinear_Distortion.html(en "soft clipper")


Vi ser at for små inngangsverdier er funksjonen lineær. For større inngangsverdier introduserer vi progressivt mer klipping. Dette kan være f.eks en rørforsterker som ikke har uendelig utgangsspenning.

-k

FIR vs IIR-filtre
Til romkorreksjon, digitale equalizere, filtrering i oversamplende AD/DA etc bruker man gjerne variasjoner over samme grunnstruktur, et generelt digitalt filter som enten har uendelig impulsrespons (som et rom eller kondensator) eller endelig impulsrespons (som et ekko eller en refleksjon).


Denne tegningen er illustrerer prinsippet. Den viser et 2.ordens, Direkte form 2 blokkskjema for et IIR-filter.  

Signalet x flyter inn fra venstre, og filtrert signal y flyter ut til høyre. "n" er en diskret tidsvariabel (samplet).  z^-1 representerer en forsinkelse på et sample. b1 og b2 er enklest å forstå og representerer "foroverdelen" av filteret.  

Et FIR-filter har bare slike b1.....bM hvor M er filterets lengde og a1...aN er altså lik 0. Da ser vi at vi ved tidspunkt n har tilgang på x, x(n-1) og x(n-2) (for skjemaet over). ved å variere b1 og b2 kan vi da få forskjellige filterfunksjoner. Det trivielle tilfellet er b1=b2=0,

y = x

og da har vi et filter som ikke gjør noe som helst. ved å øke b1 til 1 summerer vi nåværende sample med forrige sample og har en enkel interpolasjon som glatter ut kurven (lav-passfunksjon).

y = x + x(n-1)

Bytter vi b1 til -1 tar vi differansen mellom nåværende og forrige sample, altså en form for derivasjon (kurveformens helling) som provoserer fram endring, et høypassfilter.

y = x - x(n-1)

Det burde være enkelt å se at ved å gjøre M veldig stor kan vi få en impulsrespons på 1 sekund ved 44.1kHz ved å ha M = 44100 "tapper", og da kan vi gjøre mye i det vi subjektivt klassifiserer som "tidsdomenet".

y = x + b1*x(n-1) b2*x(n-2) + b3*x(n-3) + ... + bM*x(n-M)

Et IIR-filter har både slike b1.....bM og a1...aN ulik 0. For nå kan vi anta at b1...bM = 0 for enkelhets-skyld. Dette gir en tilbakekobling hvor tilbakekoblingsgrenen (venstre halvdel i blokkskjemaet) effektivt jobber med tidligere utgangsverdier, u som er ulik x. Dette er en karakteristikk som er betydelig nærmere hvordan mange fysiske systemer som masse-fjær og elektroniske kretser fungerer. Tenk på utladning av en kondensator. Dette kan modelleres som et uendelig langt FIR filter, eller som et enkelt IIR-filter hvor a1 har en passende verdi.  

y = x - a*y(n-1)


http://cnx.org/content/m10025/latest/

-k

Støyaktig jitter vil føre til en generell heving av støygulvet til AD- eller DA-konverteren. Beregning av det resulterende støynivået er noe mer komplisert, men generelt for de jitternivåer man finner i gode CD-spillere er bidraget -110dB relativt til fullt signalnivå eller lavere.

Klikk for å utvide...

Når du snakker om jitter her, så mener du jitter i den gjenvundne klokka, enten den overføres separat eller hentes fra lydstrømmen?

Altså vil ikke store mengder jitter på spdif-kabelen nødvendigvis medføre noe som helst endring av analogsignal ut av D/A med mindre :
-ei klokke gjenvinnes synkront med datatakten inn
-D/A klokkes synkront med denne

Hvis man kan fjerne fluktuasjoner fra gjenvunnet klokke (vha PLL eller et enkelt filter med lang tidskonstant), eller kjøre D/A på en lokal klokke helt asynkront med datastrømmen, vil jitter på inngang ikke medføre heving av støygulv etc. I verste fall vil D/A drifte så langt fra innkommende bitstrøm at man får buffer over/under-flyt og må kaste/putte inn en sample hver time, hver mnd eller hvert 100. år, avhengig av bufferstørrelse og differanse i midlere klokkeavvik?

-k

Vi snakker om samplingsjitter, dvs avvik i sampleperioden til DA-konverteren. Signalavhengig SP-dif jitter kan være en kilde til samplingsjitter, dog kan denne undertrykkes med en PLL e.l. Fra jitterkilde X (feks SP-dif) til samplingsjitter har man en JTF (jitter transfer function) som avhenger helt av designet til klokkekretsløpet. Hvor mye forvrenging en viss mengde samplingsjitter gir avhenger videre av designet til DACen (antall bit, aggressivitet til delta-sigma modulator, switch-cap vs. kontinuerlig tid etc).

Digital volumkontroll - bedre eller dårligere enn å dempe etter D/A-konverter?

Diskutert her:
http://www.hifisentralen.no/cgi/yab...teori;action=display;num=1139401585;start=0#0


Problemstilling:
Vi har en gitt kjede av hifi-komponenter som brukes til reproduksjon av ferdig innspilt lyd. Flere komponenter introduserer støy, og flere kan brukes til å dempe signalstyrke.

Av praktiske hensyn ønsker vi å lytte på forskjellig lydnivå avhengig av om det er fest på lørdag eller stearinlys-aften med dama. Digital volumkontroll kan ha ergonomiske fordeler kontra analog. Hva skal vi bruke?

Vi antar at sluttresultatet er det vi er opptatt av. Forholdet mellom ønsket signal, S og Total støy, Ntot gir Signal-til-støyforhold, SNR. Som lyttere er vi opptatt av både absolutt støynivå og SNR, siden vi sannsynligvis har en nedre hørbarhets-terskel for støy som kan forskyves hvis et sterkt signal blandes inn (maskering).

Digital volumkontroll forutsettes utført med ideell dithering.


Signal:
S = X * Ad * Ae

Støy-bidrag:
Nd * Ae
Ne1 * Ae
Ne2
Na

Vi antar ukorrelert støy og dermed effekt-addisjon:
Ntot = {(Nd*Ae)^2 + (Ne1*Ae)^2 + Ne2^2 + Na^2}^(1/2)
={(Nd^2+Ne1^2)*Ae^2 + (Ne2^2 + Na^2)}^(1/2)

rydder opp:
N1^2 = (Nd^2+Ne1^2)
N2^2 = (Ne2^2 + Na^2)

og får:
Ntot = {N1^2*Ae^2 + N2^2}^(1/2)

SNR:
S/Ntot = X*Ad*Ae/{N1^2*Ae^2 + N2^2}^(1/2)

Konklusjon:
Som forventet vil både digital og analog volumkontroll resultere i endret signal-nivå. Bare analog volumkontroll vil påvirke støy-nivå.

Hvis digital støy og analog støy før pot-meter (N1) er signifikant i forhold til støy i effekt-forsterker og akustisk støy(N2), forventer vi at aktiv bruk av analog volum-pot vil gi bedre SNR i rommet. Hvis totalt støybilde domineres av støy etter analog volum-pot, er det likegyldig hvorvidt vi benytter analog eller digital volumregulering.

Hvis vi skal dempe volumet kraftig ned vil dette uansett gå utover SNR siden N2 før eller senere blir dominant (i praksis som regel "før", og ikke "senere"). Dette er ikke  noe problem hvis total støy er under nedre hørbare terskel.

Den suverent dårligste taktikken er å dempe kraftig digitalt (Ad) for så å innføre positiv gain for å kompensere (Ae>1). Da vil vi først miste SNR i det digitale domenet, for så å forsterke opp støyen (og signalet) analogt.

mvh
Knut

-k

Virkelig interessant lesning dette, men absolutt ikke å anbefale som rødvins-lekture.

Lettfattelig om digital volumkontroll/gainmatching:
http://wiki.slimdevices.com/index.cgi?ConnectToPowerAmp

-k

Ivar skriver:
Dempingsfaktor: En forsterkers utgangsimpedans normalisert til en gitt last, som oftest 8ohm. Ergo; har forsterkeren dempingsfaktor 100 er utgangsimpedansen 8ohm/100 = 0.08ohm.
***********************************************

Hm, er ikke helt rett det der.
Dempningsfaktoren er faktisk hvor effektiv dempning det som står påkoplet terminalene på høyttaleren er til å dempe ned uønskede svingninger. Når en stortromme er slått til med trommistens fot, stopper skinnet etter noe få svingninger. Da skal også forsterkren trå til og stoppe høyttalermembranen fortere enn det hadde klart på egenhånd. Forsterkeren bremser altså bevegelsene. Mange tror at forsterkeren bare skubber på elementene, men den bremser faktisk også på uønskede svingninger.

Dette kan alle teste med følgende test:
Press et basselement fort inn med forsterkeren avslått. Gjør det samme med forsterkeren påslått. Du vil merke hvor mye mer bassen stritter imot med forsterkeren på. Dette er Q-faktor i praksis. Da forstår vi bedre ordet dempningsfaktor. Til høyere tall, dess mer stritter bassen imot bevegelsene som vi lager.

En høyttalerkabel vil redusere denne Q-faktoren. Høyttalerteminalene ser inn i en dempningsmotstandsverdi av summen av utgangresistansen i forsterkeren og høyttalerkablene sin resistans.

Så i det eksempelet du lagde, så blir 0,08 ohm summen av utgangsresistans i forsterkeren og kablenes resistans.

Du skriver impedans, tja, det er jo egenlig rettere det, men da blir det faktisk enda mer komplisert. Så det her blir faktisk meget komplisert matematikk med fasevinkler og korrigeringer om en faktisk skal regne og definere det helt nøyaktig. Derfor kaller jeg det bare resistanser for å forenkle det litt. Og feilen blir ikke så stor heller.

Jeg kan derfor sette opp følgende formel for Q-faktoren:

Q=Hr/(Kr+Fr)

Hr=Høyttalerresistans
Kr=Kabelresistans (husk at det er summen av de to lederne, kalt - og + leder)
Fr=Forsterkerresistans i utgangen

Legg også merke til at om en har 4 ohms høyttaler istedenfor 8 ohm, blir Q-faktoren dobbelt så dårlig.

På gode forsterkere er ofte utgangsresistansen så lav som 0,1 ohm eller lavere. En bør da prøve å ha så tykke kabler at en har 10 ganger lavere kabelresistans på summen av - og + lederen enn det som forsterkeren har på utgangen. Dvs. 0,01 ohm. Dette gir ofte tykke kabler på 3 meters lengde. Dere som liker å regne, kan jo da regne ut hvor tykke kobberledninger må være, altså kvadratet. Først da ødelegger ikke kablene Q-faktoren vesentlig.

Husk at reell Q-faktor faktisk er det terminalene på høyttaleren ser inn i. Det er jo dette som gir den reelle dempningsfaktoren. Vet at det er mange lærebøker som definerer dette feil. Men nå har dere den sanne forklaringen på det hele.

Mvh Consen
(En tidligere lærer for de som skulle bli radio/tv-reparatører).

o.t.

consen skrev:

Ivar skriver:
Dempingsfaktor: En forsterkers utgangsimpedans normalisert til en gitt last, som oftest 8ohm. Ergo; har forsterkeren dempingsfaktor 100 er utgangsimpedansen 8ohm/100 = 0.08ohm.
***********************************************

Hm, er ikke helt rett det der.
...

Klikk for å utvide...

... alt avhenger av betraktningsvinkel og hvilken historie man ønsker å fortelle.

Historien til en forsterkerprodusent er dempingsfaktoren levert på utgangsterminalene til et forsterker trinn.
Historien til en HT-produsent handler mye av bassavstemming - resonansfrekvense(er), impedans, impulsresons, Q-verdi osv.

«Reell» dempingsfaktor er den som finnes på terminalene til HT-elementet, og da er kjeden noe lengre enn den du har beskrevet, hvor de viktigste bidragsyterne sannsynligvis er serieelementene i delefilteret. Det jeg skulle ha likt å se er en lett forståelig beskrivelse av sammeneheng evt. mangel på sådan mellom dempingsfaktor og HTs bassavstemming.

mvh
KJ

KJ: Du har skjønt det hele forstår jeg ;D
Det er bra. Men da forstår du også at skytestrenghøyttalerkabler ødelegger den.
Q-faktoren er viktigst på lave frekvenser, og der er spolen til basselementet nesten i kortslutning. Og interne kabler inne i kassen er så korte at de betyr ikke all verdenn, nesten selv om det hadde vært skytestreng. OK. Den siste var litt overdrevent.

I diskanten snakker man overhodet ikke om q-faktor. Normalt ikke om mellomtone heller. Tregheten i naturen er begynner å bli for stor.
Et basselement har sin egenfrekvens. Den er nesten konstant. Den påvirkes derfor nesten ikke av q-faktoren. Høy q-faktor drar den litt ned, me nesten ikke noe. Men kabinettet påvirker den i større grad. Eller kan påvirke den skulle jeg heller hatt skrevet. Større egenvekt gir lavere resonansfrekvens.

Bare tenk på pianoet, de tykkeste strengene svinger i lavest frekvens. Dempes de litt, endres frekvensen litt, men nesten ikke noe. Det er strammingen og massen som nesten alene bestemmer frekvensen, slik er en høyttaler også.

Mvh Consen

Ivar_Loekken skrev:

(...)
Aliasing: Hvis man prøver å sample et signal over nyquist-frekvensen, vil dette føre til et uønsket alias like langt under nyquist-frekvensen som det opprinnelige signalet var over. Man sier at signaler som samples foldes rundt nyquist-frekvensen. For å unngå uønsket aliasing ved sampling, må alt signalinnhold over nyquist-frekvensen filtreres vekk først (kalt antialiasing eller antialias-filter).
(...)

Klikk for å utvide...

Artig illustrasjon under. For bildeopptaket er samplingsfrekvens lik frame-rate (30 eller 60 hertz) og det er ikke noe antialias-filter på bilderammer. Derfor gir strengene som vibrerer høyt over Nyquistfrekvensen lavfrekvent visuell aliasing.