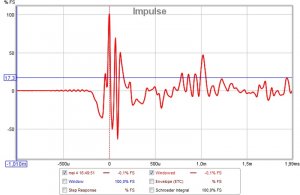
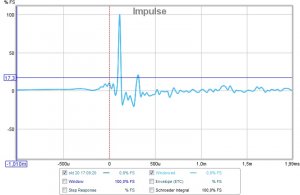
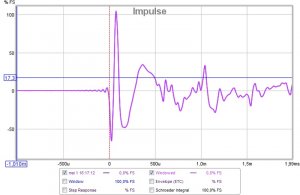
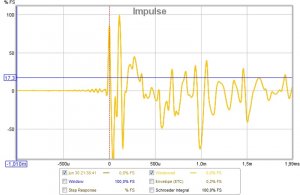
Matematisk sett gir dette ingen tilleggsinformasjon utover frekvensresponsen. Det er bare to måter å se samme virkelighet på, hhv i tids- og frekvensdomenet. Enkleste måte å forstå det på er å forestille seg en ren sinusbølge ved en gitt frekvens. I frekvensdomenet er den en impuls ved den aktuelle frekvensen, mens i tidsdomenet er den en sinuskurve som funksjon av tid. Motsatt vil en skarp impuls i tidsdomenet være et bredt spektrum i frekvensdomenet. Måleprogrammer vil typisk generere frekvenskurve fra impulsmåling eller motsatt, slik at du slipper å gjøre to separate målinger av samme sak.
Når det er sagt, virker det som om øret ikke er helt enig. Mitt inntrykk er at forløpet i de første millisekundene også påvirker lokalisering av lydkilden og en mer ubestemmelig følelse av "virkelighet". Deretter følger en periode hvor øret (dvs hjernen) "integrerer opp" energien over litt tid til et helhetsinntrykk av tonalitet, før den til slutt er i stand til å skille ut en refleksjon som et distinkt ekko adskilt fra det første signalet. Derfor synes jeg det er nyttig å se begge fremstillingene, både frekvensgang og impuls, ettersom de oppleves som ganske forskjellige ting.
Dessuten kan man lese en del tekniske ting rett ut av impulskurven, såsom fasefeil eller tidsforsinkelse mellom bass- og diskantelement, refleksjoner fra baffel/gulv/vegger/tak, osv. Hvis man ser en refleksjon etter 1,0 ms, vet man jo at den refleksjonen hadde 34 cm lenger reisevei enn direktelyden (lydens hastighet er 340 m/s = 340 mm/ms = 34 cm/ms), og da er det ikke så vanskelig å gjette at dette kanskje er kanten på baffelen i en eller annen retning. Det er ikke like opplagt å lese det samme ut av en frekvensgang som viser en bølgedal ved 500 Hz, selv om nøyaktig den samme informasjonen er innebakt i kurven.