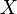Sannelig. Wikipedia tar feil igjen: Les bare her:
"Reaktans kalles den delen av impedansen som er reaktiv.
Den andre delen kalles resistans.
Betegnelsen er
og måleenheten er Ohm, [
]. En negativ reaktans er kapasitiv, en positiv reaktans er induktiv."
Reaktans - Wikipedia
Er det ikke grusomt? 
Det er meget muligt de tager fejl, men jeg har ikke skrevet hele historien for at bevare en klarhed om hvad dette her drejer sig om.
Og jeg er bange for at du bliver mere forvirret af dette her, men om ikke andet så måske forvirret på et højre niveau

.
Men som Hi-Fi-akustik sagde er reaktans den imaginær del .
I en kondensator er der fasedrej, spændingen er 90 bagud i forhold til strømmen , det vi sige at den reaktans Xc vi regner ud er ikke sammenlignelig med en almindelig modstand hvor spænding og strøm er i samme fase.
Det samme gør sig gældende med spolen, dens Ac modstand reaktans kan også beregnes, den benævnes Xl, Xl har følgende formel Xl =2*PI*f*L f i Hertz og L i henry , spolen har også fasedrej, her er spændingen bare 90 grader forud for strømmen.
Har man en situation hvor man skal beregne den samlede impedans af nedenstående kredsløb, så bruge man noget som hedder kompleks regning , hvor hvert tal består af en real del/komponent uden fasedrej, og en imaginær del med fasedrej på formen z= a+jb, formen z= a+ib ses også, denne form kaldes rektangulær form. Men kan også angive på polær/vinkel form:
. Se længere nede i teksten hvordan denne form beregnes udfra rektangulær form
Skal man regne Z ud ved et 1 KHz i ovenstående kredsløb så kan der startes med at beregne de to imaginære modstande/reaktanser Xc og Xl.
C3 Xc= 1/2*PI*f*C -> 1/2*PI*1000* 100nF = 1.59K og for L1 Xl =2*PI*f*L -> 2*PI*1000*100mH = 628ohm
Og der lægges sammen på a+jb form, det ses at kondensatorer for negativt fortegn og spoler positivt fortegn fordi de har henholdsvis -90° og +90° fasedrej:
Z = 1K - j1.59K + 1K + j628 = 2K - j962 på rektangulær form* , det giver på den mere forstårlige polær/vinkel form
2.22K -25.69° (fasedrej),
Den reelle numeriske del modulus beregnes således: kvadratrod( a^2+b^2) = 2.22 Kohm , og argumentet vinklen beregnes således arc (Z) = arc tg (b/a) = -25.69°
Det har nok forvirret mere end oplyst, men pointen er at begreberne Xc og Xl ikke er sammenlignelige med almindelige modstande uden fasedrej .
Der skal en bestemt regnemetode til at regne på kredsløb med komponenter som har reaktans, (bl.a. spoler og kondensatorer).
Gudskelov har man maskiner til dette, men i gamle dage sad man faktisk og regnede hver eneste punkt ud på et bodeplot (en frekvenskurve), det tog en krig.
I dag tager det et mikrosekund med en simulering program , og programmet laver ingen fejl.
* to z lægges sammen på følgende måde z1+z2 hvor z1= a1+jb1 og z2= a2+jb2 -> z1+z2 =(a1+jb1)+(a2+jb2) = (a1+a2) +j(b1+b2) , man addere real-delene og imaginær-delene hver for sig.
Sådan findes der regneregler for division, subtraktion, gange, kvadratrod osv. som er gældende for komplekse tal, man kan selv studerer viderer hvis det har interesse
http://da.wikipedia.org/wiki/Komplekse_tal
Gider man ikke regne i hånden så findes der regnemaskiner som kan regne med komplekse tal, bruger selv en HP42, som i dag kan downloades til PC, så man ikke behøver have den i fysisk form
http://thomasokken.com/free42/ og såmænd fås den også til Android
https://play.google.com/store/apps/details?id=com.thomasokken.free42
Man skal være opmærksom på at HP42 bruger
omvendt polsk notation OPN og er man ikke bekendt med dette indtastningssystem, så kan det nok volde problemer.
Men ellers er HP42 god til complex regning.
Der findes også online regnemaskine som regne med komplekse tal, søg selv
https://www.google.dk/search?client...ie=UTF-8&oe=UTF-8#q=complex+calculator+online