ChatGPT kommer til å gi oss verdensfreden til slutt! Sanna mina ord!Vet ikke hvor populært det er å spamme denne tråden med ChatGPT tekster, men jeg synes også dette er godt forklart, og kan kanskje hjelpe flere med å oppklare forskjeller mellom fase og tid. Det viser også hvorfor det å bruke aktiv deling og digitale FIR filtre er 1000% ganger kulere enn å leke med kabler. (Hvis man er opptatt av timing da)
Dette er en klassisk diskusjon innen akustikk og signalbehandling: Hva er forskjellen på faseforskyvning og tidsforsinkelse? La oss gå gjennom dette punkt for punkt.
1. Faseforskyvning vs. Tidsforsinkelse – Definisjoner
Tidsforsinkelse (Delay)
- En konstant forsinkelse på et signal betyr at hele signalet (uansett frekvens) blir flyttet i tid, for eksempel hvis en høyttaler spiller en lyd litt senere enn en annen.
- Måles i sekunder (s), millisekunder (ms) eller nanosekunder (ns).
- Påvirker alle frekvenser likt – hele signalet blir utsatt for samme forsinkelse.
Faseforskyvning (Phase Shift)
2. Kommentar til Person 1
- En faseforskyvning betyr at forsinkelsen varierer med frekvens.
- Måles i grader (°) eller radianer (π) og gjelder kun for periodiske signaler.
- Påvirker ulike frekvenser forskjellig, noe som kan forvrenge signalets form.
- Vanlig i delefiltre og høyttalere, der lav- og høyfrekvente signaler får forskjellige faser.
Person 1 nevner at tidstapet i en 2,5 m kabel er på nanosekund-nivå og dermed ubetydelig sammenlignet med tidsforskjellene som oppstår i et passivt delefilter. Dette er korrekt.
Hvorfor?
Konklusjon: Kabelforsinkelsen er ubetydelig sammenlignet med delefilterets effekter.
- I en standard kobberkabel er signalhastigheten typisk 200–250 millioner m/s.
- En kabel på 2,5 meter gir da en forsinkelse på ca. 10–12 nanosekunder (ns).
- Til sammenligning gir et passivt delefilter ofte millisekund-forsinkelser, altså 100 000 ganger større forsinkelse!
3. Kommentar til Person 2
Person 2 sier at passive delefiltre ikke har tidstap, kun faseforskyvning. Dette er delvis feil.
Person 2 hevder også at fase ikke er hørbar. Dette er ikke helt korrekt:
- Ja, delefiltre gir faseforskyvning, fordi de påvirker ulike frekvenser forskjellig.
- Men faseforskyvning kan også føre til effektiv tidsforsinkelse for komplekse signaler, særlig transienter (korte lydpulser).
4. Hva skjer med en transient (kort lydpuls)?
- Ved enkle sinuskurver er faseforskjeller ofte umerkelige.
- Men i musikksignaler, der mange frekvenser kombineres, kan faseforskjøvet informasjon påvirke transienter og skape hørbare forskjeller, spesielt i stereoperspektiv.
Ren tidsforsinkelse: Hele transienten flyttes i tid, men beholdes uforandret.
Faseforskyvning: Ulike frekvenser i transienten forskyves forskjellig, og lydbildet kan endres.
→ Hvis et passivt delefilter faseforskyver transienten nok, vil det oppleves som en tidsforsinkelse – særlig i høyttalersystemer. Dette er hvorfor tidskoordinering i høyttaleroppsett er viktig.
5. Konklusjon
Person 1 har rett i at tidsforsinkelsen i en kabel er ubetydelig sammenlignet med et delefilter.
Person 2 tar feil i at et passivt delefilter ikke gir tidsforsinkelse – faseforskyvning kan føre til effektiv tidsforsinkelse, spesielt for transienter.
Fase og tidsforsinkelse er nært beslektet.
- Faseforskyvning betyr at forsinkelsen er frekvensavhengig.
- Tidsforsinkelse betyr at hele signalet flyttes i tid uten å endre form.
- I musikk er faseforskyvning hørbar når den påvirker transienter og timing i signalet.
Digitale avspillere dCS Varése Dac...en ny standard innen digital lyd
- Trådstarter Espen R
- Startdato
Diskusjonstråd Se tråd i gallerivisning
-
Stereophile har en artikkel i dag om at high-end firmaet Krell har ligget i dvale i et halvt år etter at sjefen sjøl brått døde i juni sist år. Et lite familiedrevet foretak hvor eierandeler og penger blir et tema for etterkommere. Servicedelen på produktene har også vært i dvale i denne perioden.
En reminder om den risikoen vi løper ved å kjøpe dyre produkter fra sånne små bedrifter hvor alt hviler på et par mennesker, det være seg Krell, dCS eller andre.
Økonomisk sett er de fleste av disse små firmaene ganske presset, vil jeg tro.
Sist redigert:Flott oppsummering av @Armand her. Men for å komplisere videre så gir også geometrien av elementer på baffel mulighet til denne type forskyvning (husk Pythagoras), også plassering av voice-coil på hvert av elementene og elementene sin naturlige avrulling (IIR filter i seg selv). Så det er mange momenter å ta med for å forstå dette helt til "bånns". Jeg setter derfor spørsmålstegn ved momenter jeg ser på som små, som: relevansen av tidsforskjeller i kabler, SINAD 115 mot 120, eller THD 0.01 mot 0.0001. Jeg mener at slaget om god lyd utkjempes på andre arenaer.- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Jeg skal ikke bruke ordet/analogien hoppetau i audiosammenheng flere ganger. Lover.
Men at impedansoverganger ikke kan utlignes momentant, dvs at det skjer absorpsjon og refleksjon er ikke noe som plutselig skjer med 10% av kabellengden eller noe sånt. Det skjer ved alle dv/dt (endringer).
Slik tenker jeg på når jeg vurderer produkter, derfor holder jeg meg ganske mainstream og kjedelig og velger Technics, McIntosh etc fremfor små eksotiske merker, med ganske begrenset forhandler og servicenettverk og ikke minst usikker langsiktig soliditet.Stereophile har en artikkel i dag om at high-end firmaet Krell har ligget i dvale i et halvt år etter at sjefen sjøl brått døde i juni sist år. Et lite familiedrevet foretak hvor eierandeler og penger blir et tema for etterkommere. Servicedelen på produktene har også vært i dvale i denne perioden.
En reminder om den risikoen vi løper ved å kjøpe dyre produkter fra sånne små bedrifter hvor alt hviler på et par mennesker, det være seg Krell, dCS eller andre.
Økonomisk sett er de fleste av disse små firmaene ganske presset, vil jeg tro.
- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Geometrien av elementer gir en tidsforskyvning som er lik for alle frekvenser. Altså tidforskyves en 50hz like mye i sekunder som en 20 kHz. Eller alt etter hvordan det enkelte element gjenngir hvilken frekvens og hvordan man flytter dem innebyrdes.Flott oppsummering av @Armand her. Men for å komplisere videre så gir også geometrien av elementer på baffel mulighet til denne type forskyvning (husk Pythagoras), også plassering av voice-coil på hvert av elementene og elementene sin naturlige avrulling (IIR filter i seg selv). Så det er mange momenter å ta med for å forstå dette helt til "bånns". Jeg setter derfor spørsmålstegn ved momenter jeg ser på som små, som: relevansen av tidsforskjeller i kabler, SINAD 115 mot 120, eller THD 0.01 mot 0.0001. Jeg mener at slaget om god lyd utkjempes på andre arenaer.
Et delefilter består av RLC elementer og gir faseforsjeller hvor tidsforskjellene er ulike for hver enkelt frekvens. En 50 hz som er 10 grader forskjøvet og en 20 khz som er 10 grader forskjøvet er to helt ulike tider.
Ohms akustiske lov gjelder også. Man hører ikke fase. Ohm's acoustic law - Wikipedia
Så du tenker forsterker => høyttaler grensesnittet er en tabbe? Har du forsøkt å regne på attenuasjonen av en refleksjon, forårsaket av 1/100 bølge?Jeg skal ikke bruke ordet/analogien hoppetau i audiosammenheng flere ganger. Lover.
Men at impedansoverganger ikke kan utlignes momentant, dvs at det skjer absorpsjon og refleksjon er ikke noe som plutselig skjer med 10% av kabellengden eller noe sånt. Det skjer ved alle dv/dt (endringer).
Nei, vi kan nok trygt betrakte alt i vår verden som rene partikkelledere og forholde oss til enkle LCR beregninger + støy
Samme betraktninger. F eks når jeg kjøpte min Yamaha forsterker, så fikk jeg høre det av høvdingen på en av high-and sjappene som syns det var modig gjort av meg å bruke 70k på en Yamaha forsterker med tanke på annenhåndsmarkedet og den statusen Yamaha har i high-end miljøet i Norge.Slik tenker jeg på når jeg vurderer produkter, derfor holder jeg meg ganske mainstream og kjedelig og velger Technics, McIntosh etc fremfor små eksotiske merker, med ganske begrenset forhandler og servicenettverk og ikke minst usikker langsiktig soliditet.
Akkurat den betraktningen ga meg dobbelt så god samvittighet ved å ha kjøpt produktet!- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Attenuasjonen kan vi nok trygt se bort fra.Så du tenker forsterker => høyttaler grensesnittet er en tabbe? Har du forsøkt å regne på attenuasjonen av en refleksjon, forårsaket av 1/100 bølge?
Nei, vi kan nok trygt betrakte alt i vår verden som rene partikkelledere og forholde oss til enkle LCR beregninger + støy
Og vi kan jo forstå dette før vi eventuelt forkaster det. Er det innenfor 4-10 us på transient og 10-100 us delay så kan det spille inn. Øret forsterker 40 db etter en transient. Det er en ganske bra forsterker vi har der.
Vil ikke det være tilstrekkelig i de aller fleste tilfeller der man ikke viser til noe som er direkte ukjent og kontroversielt? Kan man ikke eventuelt be om referanser til aktuell forskning om det skulle behøves?En typisk feil er å henvise til at "forskning viser....", men uten å sette dette i kontekst, og slik hoppe over signifikans
For eksempel har vi jo mange ganger sett en kurve som viser fordelingen av ulike lytteres ytelse i en ABX-test kategorisert på om de har en rolle i hifibransjen, der verken forhandlere, produsent-representanter eller audiofile kom særlig godt ut av det. Men denne har vært postet så mange ganger at selv om datagrunnlaget ikke er stort nok så bør man vel kanskje kunne støtte seg på denne som allmenkunnskap i dag? Selv husker jeg ikke om det er Harman, Toole eller noen andre som er den egentlige kilden bak.
Det er vel i grunn godt forstått, da dette ikke bare kan fremstilles matematisk, men også med høy nøyaktighet måles. Faktisk fascinerende å måle effekten av forskjellige fenomener på bølgeledere. Bølgeledere er ikke som andre ledere...Attenuasjonen kan vi nok trygt se bort fra.
Og vi kan jo forstå dette før vi eventuelt forkaster det. Er det innenfor 4-10 us på transient og 10-100 så kan det spille inn.
Synes vi uansett kan skille mellom bølge- og partikkelleder i hvordan vi betrakter det hele. Men for all del, finner du noe nytt, er vel dørene åpne for en hver å presentere et paper på det. Personlig har jeg nok slått meg til ro med skoleengelsken og skal slutte å forstyrre..
Personlig har jeg nok slått meg til ro med skoleengelsken og skal slutte å forstyrre..
Typisk ABX testing med korte og hyppige vekslinger er uegnet til å vurdere nyanseforskjeller i lyden. Som argument for at «alt låter likt» er det imidlertid velegnet.For eksempel har vi jo mange ganger sett en kurve som viser fordelingen av ulike lytteres ytelse i en ABX-test kategorisert på om de har en rolle i hifibransjen, der verken forhandlere, produsent-representanter eller audiofile kom særlig godt ut av det.
Hvis utgangspunktet er feil, at det er en eller annen feil i hypotesen, at det er noe som ikke er tatt med i regnestykket, så vil resultatet nødvendigvis ikke bli riktig. Så kan man krangle i det uendelige om hvem som har bevisbyrden i den ene eller andre retningen. Og om det virkelig er sånn at vi er allvitende i 2025, relatert til emnet.Typisk ABX testing med korte og hyppige vekslinger er uegnet til å vurdere nyanseforskjeller i lyden. Som argument for at «alt låter likt» er det imidlertid velegnet.
Det er ingen som setter krav til at du må gjennomføre slike tester med korte og hyppige intervaller.Typisk ABX testing med korte og hyppige vekslinger er uegnet til å vurdere nyanseforskjeller i lyden. Som argument for at «alt låter likt» er det imidlertid velegnet.
Hør gjerne 1 uke eller mer på hver, men poenget er at du ikke skal vite hva som er hva når du velger. -Aka det er ørene som skal være grunnlaget for valget.
Men det er jo klart at de som er mest imot slike tester, ofte er de samme som frykter resultatet.
Jeg synes hoppetau-analogien er ganske god for å intuitivt forstå hvorfor man må ha plass til minst én halv bølgelengde for å kunne få til en refleksjon. Siden mottakerenden ikke er aktiv må den være festet til en vegg. Men det er ett stort problem her, og det er at i denne analogien er impedansen i mottakerenden null, og selve tauet har svært høy impedans. I den virkelige verden har man et resistivt tapselement i mottakerenden, og impedansen i selve tauet er så lav at LCR-parametrene er neglisjerbare.Du skriver her om kvartbølger og halvbølger. Altså i hoppetau analogien om når hele bevegelser stanser og nuller seg ut. Dette er ikke relevant selvsagt. Alle audio kabler leverer signal. Ingen som hevder at det stopper opp.
En bedre analogi vil derfor være som følger:
Vi bytte ut tauet med et 0,2 meter langt 10mm armeringsjern.
Frekvensen er opp til 1Hz.
Armeringsjernet er montert vertikalt og mottaksenden er en bøtte med honning, altså et betydelig tapselement som allikevel gir armeringsjernet bevegelsesfrihet.
Dersom vi analyserer dette oppsettet for opp til 1kHz vil vi se at vi kan finne frekvenser som gir ringing grunnet armeringsjernets induktans (masse) og kapasistans (elastitet). Samtidig ser vi at tapselementet i mottaksenden får ringingen til å dø ut ganske raskt. Vi ser også at frekvenser opp til 1Hz aldri er i nærheten av å gjøre ringingen relevant. Vi ser videre at siden armeringsjernet er så kort så er ikke refleksjon en aktuell måte å beskrive oppførselen ved lave frekvenser. Det samme gjelder ved 1kHz, selv om vi der trolig har funnet en reaktiv mode på veien. Med andre ord, vi må ikke begynne å blande inn refleksjoner med en gang vi finner en reaktiv mode.
Vi ser også at strategisk plassering av, og kalibrering av tapselementer som funksjon av frekvens og impedans i kabelen hjelper oss til å stabilisere signaloverføringen. Dette er det som kalles transmissjonsteori og brukes ved beregning av avsender, mottaker og kabelimpedans til et gitt formål. For eksempel bruker vi i ethernet en overføringsfrekvens på opp mot 375MHz overført i TP-kabler (Twisted pair). Det interessante her er at dette er stabilt på en meter, og på 80 meter, fordi man ikke bare har et tapselement i hver ende, men også et linjært tapselement gjennom hele kabelen som gjør at både tapselementet og de reaktive komponentene er en funksjon av lengden på kabelen. Ganske enkelt og allikevel snedig. Slik tankegang skal du nok lete lenge etter hos hifikabelpusherne.
En av de tingene Kunchur påpeker, som er riktig, er at fase til en viss grad er hørbart. Vi er ganske sensitive for faseskift i ørets mest følsomme område. Man kan for eksempel sette opp en sammenlikning mellom et bratt delefilter med faserotasjon og ett som er fasekompensert, og man behøver ikke være veldig godt trent lytter for å høre forskjell. Den typiske subjektive vurderingen er at man får en mer rigid plassering av dybde i lydbildet. Man kan for eksempel sette på en innspilling og oppleve at vokalen trolig befinner seg noe bak høyttalerne, men vanskelig å si det helt sikkert. Så kompenserer man fasen og plutselig er den som skrudd fast til gulvet, man kan gå frem og sette et kryss, og neste lytter vil typisk reagere på samme måte. Med DSP er dette enkelt å AB-teste og det er blitt gjort utallige ganger.Et passivt delefilter har ikke tidstap. Det gir faseforskyvning og fase er ikke hørbar (nesten!!). Man må skille mellom tidsforsinkeler og fase. Fase er bare relevant for signal som gjentar seg hele tiden (som disse sinusene). Når det gjelder transienter er ikke fase relevant. Kun tiden, altså når det kommer.
Et annet eksperiment vi kan gjøre er å kjøre en "in-phase-out-of-phase" test på hodetelefoner. Man skulle tro at så lenge hvert øre bare eksponeres for én høyttaler så hører vi ikke forskjell, men den gang ei.
Ja, og det virker som om dette er noe av bristen i Kunchurs tolkning av kildene.Enig. Man kan ikke se på tidspresisjon og båndbredde som direkte ekvivalenter. Men de fleste gjør nettopp det.
I en høyttalerkabel er bølgelengden altfor lang til at vi kan snakke om refleksjoner. I tillegg er LCR-parametrene ekstremt mikroskopiske sammenliknet med LCR-parametrene i lasten. Det er stort sett bare motstander som leveres med bedre enn 5% toleranse. Det vil si at alle delefiltere har i prinsippet mange ganger større toleranseavvik enn LCR-parametrene i den tilkoblede høyttalerkabelen. I Watt/Puppy gikk signalet til diskanten gjennom høypassfilteret til mellomtonen. Det betyr at toleranseavviket i filteret typisk vil være på noen titalls mikrofarad. I tre meter høyttalerkabel hopper man typisk ikke fra mikrofarad til nanofarad, men videre til pikofarad. Eventuelt oppgir man parametrene pr kilometer. Når kablene har en milliontedel så mye kapasistans som toleranseavviket i filteret alene blir det ganske teoretisk å snakke om det. Når i tillegg lasten (i form av driveren) har enorm induktans sammenliknet med kabelen, og en mindre variasjon i induktans i kretsen ikke later til å påvirke lyden hørbart, må man nesten spørre seg hva denne jakten består i.Når det gjelder en høytalerkabel vil ikke refleksjoner sees av forstreker. De vil bare se impenansovergangene og de er det de er.
Uansett, impedanseovergang er ikke en relevant betraktning gitt verdiene og kabellengden ift det aktuelle signalet.
Nei, det er ikke korrekt tankegang. Selv om kretsens hastighet gjenspeiles i hvor mye latency vi har fra kurveform inn til kurveform ut, så vil stigetiden være så lav at for alle praktiske formål er dette, sett fra kabelens perspektiv, i praksis DC og ikke AC.Man må også huske på at enhvert signal vil være "raskt". En 50hz like rask som en 500 khz. Og enhver endring (dv/dt) vil møte impedansoverganger og noe vil absorberes og resten vil reflekteres. Det regner man på.
Hvorfor bruker du dv/dt? Altså delta hastighet over delta tid? Er ikke det bare en krøkkete måte å skrive meter på? Det er jo det som er det springende punktet ift bølgelengde og kabellengde.Min erfaring er motsatt. Jeg har nilyttet på forskjeller mellom 320kbs mp3 vs ukomprimert. De høres tilsynelatende like ut, men jeg klarte å spotte mp3 filen ved å switche hurtig frem og tilbake å høre på et 3 sekunders stykke.Fort gjort å nerde seg fullstendig inn på millisekunder fremfor å lytte til musikk, derfor drar jeg en anekdote fra mine egne opplevelser:
På Jon Lord's utgivelse "Pictured Within" synger Miller Anderson på tittellåta, og innledningsvis lurte jeg veldig på om det faktisk var Ian Gillan som sang, synes det låt farlig likt. Hørte denne låta på en lang rekke anlegg, og opplevde det samme hele tiden, det var svært likt Ian Gillan på de første strofene. Helt til Audio Note DAC 4.1X kom på besøk. Plutselig var det distinkte forskjeller på stemmene, det var lekende lett å oppfatte at dette slett IKKE var Ian Gillan.
Stemmer er det vi mennesker er aller best på å høre forskjell på. I en samtale med mange mennesker lurer man bare helt unntaksvis på hvem som prater. Hva jeg vil fram til? At teorien om "Comparison By Contrast" ikke nødvendigvis er så dum.
Sånn, tilbake til millisekundene!
Når vi snakker om latency i kabler så snakker vi om linjær forsinkelse. 1ns tilsvarer 0,35 tusendeler av en millimeter. Om du strammer skruene til diskanten 1 grad har du flyttet diskanten ca 10 ganger mer. Tenker du det er noe du hører forskjell på?Geometrien av elementer gir en tidsforskyvning som er lik for alle frekvenser. Altså tidforskyves en 50hz like mye i sekunder som en 20 kHz. Eller alt etter hvordan det enkelte element gjenngir hvilken frekvens og hvordan man flytter dem innebyrdes.
Tallforståelse er en helt sentral del av fagforståelse.
Dette er et helt annet emne. For det første er latency og group delay noe helt ulikt. Latency er shit-inn-shit-ut forsinkelse. Altså det første som går inn, uansett hva det er, vs det første som kommer ut. Group delay er en envelope funksjon av signalet. Det vil for eksempel si at om vi har et 100-ordens filter så vil det ringe ut av ville helvete. Det vil også ha en sinnssyk lang group delay som man knapt kan definere. Men latency er basically null.Et delefilter består av RLC elementer og gir faseforsjeller hvor tidsforskjellene er ulike for hver enkelt frekvens. En 50 hz som er 10 grader forskjøvet og en 20 khz som er 10 grader forskjøvet er to helt ulike tider.
Det kan vel ikke kalles hans stolteste øyeblikk, i motsetning til selve ohms lov.Ohms akustiske lov gjelder også. Man hører ikke fase. Ohm's acoustic law - Wikipedia
Denne tråden handler vel egentlig fortsatt om et produkt bygget etter ohms tredje lov, loven om obscenely high margins...- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Cyril Bateman hadde noen målinger på dette en gang på en 10 khz sinusbølge. Skal ligge i en gammel tråd her på sentralen. Ellers viste er forsker på diyaudio en gang beregninger at settling time ved ulike karakterirske kabel impedanser. Man bruker de helt vanlige formelene for absorbsjon og refleksjon rundt et impdansdsskille, så får man en kurve som trinnvis går mot at høyttaler tar last (ser riktig impedans). Da viste man settling time godt innnefor verdiene jeg nevnte. Man kan beregne forløpet like godt med bare å se på de ideele RC verdiene, men da får man ikke med seg selve fysikken bak (trinnene).^Er det refleksjonen du fremdeles mener utgjør noe her? Kan du utdype? Gjerne med beregninger.
Men like viktig. Kunchur viser til slike målinger på signalkabler og viser forløpet av to kabler i artikkelen (side 20). Men etter min mening er tidene her så korte at det er tvilsomt om dette faller innenfor verdiene 4-10 us og 10-100 us decay. Signalkabler er nok bedre matchet til lasten. En høyttaler kan være ned mot noen få ohm mens kabelen er hundre og ofte noen hundre ohm.
Siden øret forsterker 40 db etter en transient er alle forhold som kan falle inn under nevnte område interessante om dette gjelder høyttaleren selv, kabler, forsterkere eller kilde. Det er en grunn til at CA finnes Cochlear amplifier - Wikipedia.
Increased sensitivity for soft sounds altså.
Sist redigert:
Det burde være lett å bevise.Typisk ABX testing med korte og hyppige vekslinger er uegnet til å vurdere nyanseforskjeller i lyden. Som argument for at «alt låter likt» er det imidlertid velegnet.Tok et byggelån for å kjøpe signalkabler med 2 nanosekunders kortere forsinkelse, og lyden ble perfekt. Kølsvart bakgrunn, sikringsskapet åpnet seg, og naboen under oss som var lam fra håret og ned, kom løpende og sa han var blitt helbredet. Halleluja!
Så kommer selvfølgelig kjerringa hjem med tre nye pynteputer fra Jysk med kordfløyelstrekk, og da gikk lyden lukt til hælvete. Mozarts panfløytesonate høres ut som Tøyen skolekorps, førsteutgaven av Best of Celine Dion's Greatest Hits Vol. 3 høres ut som Pavarotti som har satt en hel kalkun i halsen. Og jeg kunne fortsatt.
Heldigvis finnes det masse fint lesestoff på HFS. Takk for at dere orker.Transittiden i audiokabler er typ 3-5ns pr meter - derved 0,001% av det som her påståes å være hørbart....
Motstand i signalkabler på noen hundre ohm??? det må være en bit bomulltråd innsatt med sot... slev såkalt lakris har da en mtstand på under en ohm pr meter..
Kilde og lastimpedans vil derimot være typ noen hundre ohm i kilde og helst noen titallls kohm i last...Sist redigert:Stemmer hører man oftest forskjell p ånokså enkelt.. jeg har små om ingen pproblemer med å høre forskjell på Pavarotti, Domingo, Carerras eller Kaufmann.. selv på den lille dab-radioen madam fruen har parkert på badet... trenger hverken DACer, forsterkere eller høyttalere med 4-5 sifret prislapp for den jobben- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Bare hentet noen vilkårlige data fra nettet (ikke gpt)Transittiden i audiokabler er typ 3-5ns pr meter - derved 0,001% ac det som her påståes å være hørbart....
Motstand i signalkabler på noen hundre ohm??? det må være en bit bomulltråd innsatt med sot... slev såkalt lakris har da en mtstand på under en ohm pr meter..
Kilde og lastimpedans vil derimot være typ noen hundre ohm i kilde og helst noen titallls kohm i last...
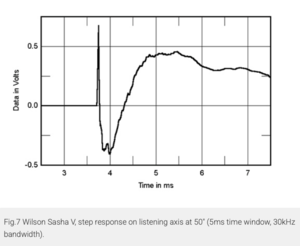
Jo men selv om tidsforskyvningen innbyrdes mellom elementene er den samme, resulterer en fast tidsforskyvning i helt ulike resultater ettersom bølgelengder varierer med frekvens. La meg prøve å illustrere med et eksempel fra høyttaler som oppgir å optimalisere tid/fase riktig posisjon av elementer. Jeg har ikke målinger på værstingen Wilson Chromosonic, så la oss nøye oss med Wilson Sasha D (kun 712.000 NOK). Her leser vi fra produsenten sin egen hjemmeside: "The upper module two-position front spike track offers additional adjustment positions the Sasha DAW doesn't have, resulting in more precise time alignment accuracy", og vi skulle jo tro at de guruene som lager dette vet hva de gjør (men det gjør de ikke, hint se målingene). Derfor har jeg også med meg en lignende usikkerhet når jeg leser om dCS DAC til 3 mill, vet de egentlig hva de holder på med, er det jug eller ekte?Geometrien av elementer gir en tidsforskyvning som er lik for alle frekvenser.Vedlegg
-
61 KB Visninger: 6
Sist redigert:
Hele poenget her er at impedans ved så korte lengder er irrelevant, da det er umulig å få selv en brøkdel av en bølge til å oppstå... derfor gjelder kun RLC som enkle og svært små verdier.... Transmisjonsteori har rett og slett null relevans i audio typ haifai.... ved langlinje overføring ( som jeg også har drevet med) fra noen hundre meter og oppover blir det en annen skål , - som også blir større og større etterhvert som lengden øker...- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Fra artikkelen (som neppe noen har lest, men gjerne vil diskutere...side 20). Dette gjelder en signalkabel og jeg mener tidene her er litt under hva som er relevant, men MYE over hva du hevder er rett. Forklar gjerne.Hele poenget her er at impedans ved så korte lengder er irrelevant, da det er umulig å få selv en brøkdel av en bølge til å oppstå... derfor gjelder kun RLC som enkle og svært små verdier.... Transmisjonsteori har rett og slett null relevans i audio typ haifai.... ved langlinje overføring ( som jeg også har drevet med) fra noen hundre meter og oppover blir det en annen skål , - som også blir større og større etterhvert som lengden øker...
This point was illustrated for audio cable characteristics in [180] and is shown here in Fig. 22: From panel (a), the 90%-to-10% fall time τfall of cable G is shorter than for cable S (τfall = 300 ns); but G has almost double the 60-dB fall time (τ60=1666 ns) compared to the τ60 = 936 ns for S (panel (b)) due to its non-ideal capacitive behavior. Furthermore, the response for S has cleanly disappeared (below this measurement’s threshold) by 1.1 µs, whereas G still has observable residue at 2.4 µs. It is important to note that this type of distortion does not show up in a frequency-spectrum measurement: the measured gains and phases varied by less than ±0.03 dB and ±0.06 degrees respectively for both cables (see Fig. 5 of [180])
Og hvordan vil du beskrive lydforskjellen du hørte de 2 formatene i mellom?Min erfaring er motsatt. Jeg har nilyttet på forskjeller mellom 320kbs mp3 vs ukomprimert. De høres tilsynelatende like ut, men jeg klarte å spotte mp3 filen ved å switche hurtig frem og tilbake å høre på et 3 sekunders stykke.
Decay-tid er noe helt annet igjen. Her kommer frekvens inn i bildet. Dette er rundt 1MHz og har ingen relevans for noe vi hører.Fra artikkelen (som neppe noen har lest, men gjerne vil diskutere...side 20). Dette gjelder en signalkabel og jeg mener tidene her er litt under hva som er relevant, men MYE over hva du hevder er rett. Forklar gjerne.
Vis vedlegget 1093775
This point was illustrated for audio cable characteristics in [180] and is shown here in Fig. 22: From panel (a), the 90%-to-10% fall time τfall of cable G is shorter than for cable S (τfall = 300 ns); but G has almost double the 60-dB fall time (τ60=1666 ns) compared to the τ60 = 936 ns for S (panel (b)) due to its non-ideal capacitive behavior. Furthermore, the response for S has cleanly disappeared (below this measurement’s threshold) by 1.1 µs, whereas G still has observable residue at 2.4 µs. It is important to note that this type of distortion does not show up in a frequency-spectrum measurement: the measured gains and phases varied by less than ±0.03 dB and ±0.06 degrees respectively for both cables (see Fig. 5 of [180])
Men det er enkelt å produsere slike resultater ved å endre på LCR. Oppgir han LCR på kablene?
Husk også at selve målesignalet ikke kan reproduseres av noe audioutstyr som noen sinne er laget.- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Selve fysikken ligger mellom impedans grenssnittene...altså kabelen. Ja, dette er gjentakende refleksjoner og man kan relatere det til frekvens på det nivået. Men for en punkt på kabelen sees dette kun som en gradvis oppbygging/nedbygging av signaler og dermed er frekvens ikke relevant. Dette er en transient og transients decay.Decay-tid er noe helt annet igjen. Her kommer frekvens inn i bildet. Dette er rundt 1MHz og har ingen relevans for noe vi hører.
Men det er enkelt å produsere slike resultater ved å endre på LCR. Oppgir han LCR på kablene?
Husk også at selve målesignalet ikke kan reproduseres av noe audioutstyr som noen sinne er laget.
Alt av data er oppgitt i [180].Men det er kanskje for mye for langt at dette med signaloverføring skal være forstått av den gemene hop. De fleste starter sin opplæring i temaet første gang de går inn i hifisjappa og får hodet pumpet full av sprøyt. Bare et fåtall av oss brant så mye for temaet at vi oppsøkte institusjoner som tegnet et vel så fantastisk bilde av hvordan det hele henger sammen, men etterprøvbart og konsekvent. Og vi vet masse om signaloverføring. Om ikke hadde vi ikke sittet her og sludret sammen.
"Barnelæra" sitter hardt i hos mange, selv om svært mange av dem innerst inne nok vet bedre. Egentlig ikke oppsiktsvekkende, mange går jo fortsatt i kjerka også.
Erfarene lyttere bør ikke gjemme seg bak denne litt tvilsomme påstanden. Faen meg nesten bare "amatører" her inne.Typisk ABX testing med korte og hyppige vekslinger er uegnet til å vurdere nyanseforskjeller i lyden. Som argument for at «alt låter likt» er det imidlertid velegnet.
Det liker gjerne tullekabelprodusentene å prøve å få deg til å tro, men hadde du lest det jeg skrev om nettverkskabler hadde du muligens forstått hvor feil den tankegangen er.Selve fysikken ligger mellom impedans grenssnittene...altså kabelen.
Nei, dette er ikke refleksjoner. Dette er decay, som i "så lang tid tok det å lade ut en kondensator gjennom en spole".Ja, dette er gjentakende refleksjoner og man kan relatere det til frekvens på det nivået.
Poenget er at utladingstiden er så mye kortere enn båndbredden til utstyret at det ikke en gang har teoretisk interesse. Dersom kabelen lades ut med 1V/ps og signalet maks kan falle med 1V/us, så faller signalet i kabelen en million ganger raskere enn i selve utstyret. Da har det ingen ting å si om man øker dette til halvannen million, eller reduserer det til en halv million.
Det har ekstremt mye mer å si om det er høy eller lav luftfuktighet den aktuelle dagen.
Nei, dette er spenningsdecay. Du må klare å skille mellom det og signaldecay, spesielt om du skal uttale deg om emnet og forsøke å "stille folk til veggs".Men for en punkt på kabelen sees dette kun som en gradvis oppbygging/nedbygging av signaler og dermed er frekvens ikke relevant. Dette er en transient og transients decay.
Eh, "Frequency tuning properties of neurons in the inferior colliculus of an FM bat"?Alt av data er oppgitt i [180].
Men det er jo andre som har gått i detalj, og i god Kunchur-ånd var det også her verre enn man nesten kunne forestille seg:
Han har sammenliknet en kabel fra XLR ut på DAC til XLR inn på pre, og en annen kabel fra RCA ut på DAC til RCA inn på pre, og kaller det kabelforskjeller. Man skal være en rimelig innbitt kunnskapsfornekter for å fortsatt ta dette makkverket seriøst.
Og for å drive spikeren tilstrekkelig dypt inn i AES-kista, dette har han fått lov til å publisere i AES.- Ble medlem
- 26.02.2013
- Innlegg
- 3.890
- Antall liker
- 3.597
Det spørs hvem som lærer dem opp. Elon Musk sin xAI er beviselig opplært på en hel del vranglære. Slik vi også ser SeepSeek er.ChatGPT kommer til å gi oss verdensfreden til slutt! Sanna mina ord!Det at forskere utgir ting selv med fagfelle-vurderinger som bekreftelser, betyr ikke at det alltid er korrekt eller sant.
https://dinside.dagbladet.no/fritid/kjempebroler-ufattelig-pinlig-1/82600350- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Det liker gjerne tullekabelprodusentene å prøve å få deg til å tro, men hadde du lest det jeg skrev om nettverkskabler hadde du muligens forstått hvor feil den tankegangen er.
Nei, dette er ikke refleksjoner. Dette er decay, som i "så lang tid tok det å lade ut en kondensator gjennom en spole". De er helt analoge.
Poenget er at utladingstiden er så mye kortere enn båndbredden til utstyret at det ikke en gang har teoretisk interesse. Dersom kabelen lades ut med 1V/ps og signalet maks kan falle med 1V/us, så faller signalet i kabelen en million ganger raskere enn i selve utstyret. Da har det ingen ting å si om man øker dette til halvannen million, eller reduserer det til en halv million. Det er et poeng. Jeg har derfor ikke relatert nettopp dette til signalkabel.
Det har ekstremt mye mer å si om det er høy eller lav luftfuktighet den aktuelle dagen. Artig
Nei, dette er spenningsdecay. Du må klare å skille mellom det og signaldecay, spesielt om du skal uttale deg om emnet og forsøke å "stille folk til veggs".
Eh, "Frequency tuning properties of neurons in the inferior colliculus of an FM bat"? Sorry, det var vist [177] gikk litt fort når jeg egentlig fulgte med hvem Glimt skulle møte.
Men det er jo andre som har gått i detalj, og i god Kunchur-ånd var det også her verre enn man nesten kunne forestille seg:
Han har sammenliknet en kabel fra XLR ut på DAC til XLR inn på pre, og en annen kabel fra RCA ut på DAC til RCA inn på pre, og kaller det kabelforskjeller. Man skal være en rimelig innbitt kunnskapsfornekter for å fortsatt ta dette makkverket seriøst. Viser likevell forløpet av decay i en signalkabel.@Powercon Det der var jo et uhell.
Kunchur sine feil virker som litt mer enn uhell. Han har åpenbart startet med konklusjonen og stort sett bare henger på alskens referanser uten relevans.
Hans 2023-artikkel har 218 referanser. Jeg har ikke rukket gjennom alle, men av de jeg har sjekket kan de deles inn i to kategorier:
1: De har ingen som helst relevans fordi de ikke sier det Kunchur hevder de sier.
2: De har relevans, men er skrevet av Kunchur selv, og er like fulle av feil som artikkelen de skal underbygge.- Ble medlem
- 20.04.2009
- Innlegg
- 7.621
- Antall liker
- 4.067
Det er et godt poeng. Men da blir dette svart opp og blir ute av verden, blir det ikke.Det at forskere utgir ting selv med fagfelle-vurderinger som bekreftelser, betyr ikke at det alltid er korrekt eller sant.
https://dinside.dagbladet.no/fritid/kjempebroler-ufattelig-pinlig-1/82600350 -
Laster inn…
Diskusjonstråd Se tråd i gallerivisning
-
-
Laster inn…