Da blir det litt som jeg fryktet. Håper Snikcers har andre kilder for sitt interessante åpningsinnlegg enn disse lydfilene.
Jaja, her finnes det ekstremt mye å ta av. Jeg er fristet til å linke til denne:
https://en.wikipedia.org/wiki/Fourier_transform#Uncertainty_principle
Men jeg skal forsøke å forklare, allikevel i frykt for at jeg gjentar veldig mye fra åpningsinnlegget:
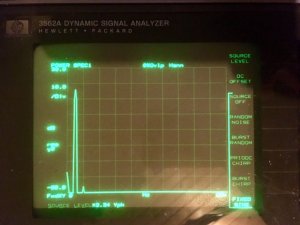
Sett at vi har en ren fullfrekvent transient. Vi får for eksempel slike fra små lyn, og slike brukes blant annet til kalibrering av målemikrofoner. En slik transient er kun begrenset av luftens egenskaper da selve gnisten er langt raskere enn luftens evne til å respondere. Dette medfører at en slik impuls inneholder alle audiofrekvenser, det vil si alle fra tilnærmet DC til der luften domineres av resistivitet og dermed ikke lenger kan transportere bølger.
En slik transient er en svært smal "spike" i tidsdomenet, og den har verken pre eller post-ringing. Dette er den korteste teoretiske pulsen vi kan skape, og den dekker altså alle tenkelige audiofrekvenser.
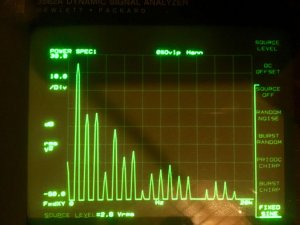
På den annen side kunne vi tenke oss en absolutt ren sinus. Men for at det skal gi mening å betrakte denne i tidsdomenet må den enten være uendelig lang, eller den må ha en eller annen form for definert start og stopp. Vi kan jo se for oss at vi begynner i null, og bare lar funksjonen reise seg ut av null-aksen, vandre noen perioder, og så stoppe like brått. Men det er på ingen måte en ren sinus. Det er hva vi kaller en Dirac-funksjon, og i knekkpunktene har vi pr definisjon alle audiofrekvenser representert. Dersom vi begynner å myke opp denne overgangen fra null til sinus vil vi redusere antallet frekvenser som er involvert, men vi vil samtidig gjøre funksjonen lenger i tidsdomenet.
I det øyeblikket det involverte antallet frekvenser intar en såkalt gaussisk fordeling, så vil også varigheten i tidsdomenet inta en gaussisk fordeling. Dette er en slags gylden middelvei for impulser og frekvenser.
Dette gir ikke rom for at vi kan betrakte musikk som "noe annet enn sinustoner". Musikk, på lik linje med alt annet, følger den ufravikelige koblingen mellom tids og frekvensdomenet, og usikkerhetsprinsippet vil alltid gjelde.
https://phys.org/news/2013-02-human-fourier-uncertainty-principle.html
Som det virker nå så vil alltid sinus(xH) starte i null på kurveformens nullpunkt.
Det høres for meg ut som om du beskriver starten på en Dirac-funksjon, stemmer det?
Hva henviser (xH) til her? Tenker du på n-te harmoniske komponenter? Når vi filtrerer ut DC så vil konsekvensen av alle harmoniske komponenter være et snitt som er lik null, men det er ikke gitt at nullpasseringen skjer på samme sted som den ville gjort uten harmonisk forvrengning.
Da blir noen av konklusjonene i startinnlegget selvoppfyllende ved at dynamikken samkjøres.
Jeg får heller ikke her tak på hva du skriver, men jeg prøver meg på en gjetning. Si i fra om det er feil:
Du ser for deg at denne enhanceren er laget slik at når signalet starter i T=0 så har det en gitt stigetid. Enhanceren får signalet til å stige raskere, og dermed øker det også dynamikken vesentlig.
Om det er det du mener, så er det et par viktige problemer med dette. For det første, siden dette er en harmonisk generator og ikke en ekspander, så kan ikke de overharmoniske komponentene respondere uendelig raskt. Se for deg en forsterker som stiger noe for raskt i starten, men går over til normalt i toppene, før den faller for bratt... osv. Det kan betraktes motsatt ved at signalet har høyere nivå, men så dempes toppene av en 3. harmonisk med motsatt fase. Realiteten er omtrent midt i mellom. Saken er imidlertid at om vi vender fasen på den 3. harmoniske så reagerer ikke ørene noe særlig på det. Vi opplever ikke at noen av signalene har endret nivå, at stigetiden er vesentlig endret, at dynamikken er endret eller liknende.
Vi kan også se for oss å filtrere dette med brick-wall filtre som altså er så bratte at vi kan klare å fullstendig isolere de to frekvensene fra hverandre. Etter filtreringen vil ikke de to frekvensene bære spor av hverandre, og man kan gjengi de to fra to ulike drivere uten at vi reagerer om fasen på den ene vendes. Ørene våre vil være interessert i frekvensspekteret.
Det blir alltid lettere definerbare hendelser i tidsdomenet, for det er slik "enhancer" virker.
Om jeg hadde rett i min tolkning av ditt innlegg over, og om du har lest forskningen jeg linket til, så tror jeg du ser at dette i langt større grad er spektrumavhengig, samt at kausaliteten er av stor betydning. Det ligger noen lydeksempler der også som jeg anbefaler deg å lytte til. Spesielt Kasablanca-kuttet, selv om det egentlig demonstrerer noe annet.
Det er ikke like sikkert at en faktisk forsterker har harmoniske som starter i null og fortsetter positivt med signalet.
Det har den nok mest sannsynlig, gitt det vi vet om hvordan forsterkere har for vane å forvrenge.
Noen ganger er det motsatt, noen ganger med en delay også vil jeg tro.
Vi kan godt se for oss at vi fasevender den 3. harmoniske i forsterkeren. Men siden den filtreres ut av et annet signal så vil vi typisk se at stigehastigheten på selve signalet ikke har blitt dårligere eller bedre, bare at vi har fått en ekspansjon i stedet for en kompresjon på toppen. Hjernen vil bare oppfatte det som en ekstra frekvens.
Legg også merke til at både effekten som omsettes og det matematiske lydtrykket er det samme.
Man kan trygt anta, utfra lignende konklusjoner som i startinnlegget, at virkningene blir annerledes da.
Hvorvidt man klarer å høre forskjell på harmonisk forvrengning med ulik fase er jeg usikker på. Så vidt jeg vet kom Earl Geddes og Lidya Lee frem til at vi ikke gjør det, og vektet derfor kun harmoniske ordener. Men jeg har ikke studert deres forskning tilstrekkelig inngående til at jeg tør å si om det var mer som burde vært undersøkt der.