Må innrømme at jeg er litt lei av disse overforenklede forklaringene.
I brake for tutorials, som kjent, og dette var nærmest en skriftlig invitasjon med rød løper og det hele.

La oss legge opp et
litt mindre overforenklet bilde av landskapet vi beveger oss i. Noen av dere har sikkert sett denne grafen før. X-aksen er frekvens, Y-aksen nivå. På venstre side regner Y-aksen nedover fra full utstyring på digitalt vis, på høyre side regner den SPL oppover. Toppen av grafen, 0 dBFS = 120 dB SPL er satt ved smerteterskelen for øret. Vi har vanligvis ikke noe ønske om å spille høyere enn det, så vi legger full digital utstyring dit og antar passe gain gjennom forsterkeri og høyttaleri til å nå 120 dB SPL i godstolen ved full utstyring.
De to blå kurvene er omrisset av et musikksignal, hvor jeg i prinsippet har dratt en kurve gjennom alle toppene i et FFT-diagram. Ordet er "envelope". Den mørke blå er gjennomsnittsnivået, den lyse er toppene, dvs gjennomsnitt + crest factor. Dette er sånn bra høyt med 85 dB SPL i snitt og 100+ dB i toppene. Den oppmerksomme vil legge merke til at vi antar at dette signalet er mastret ved ca -32 dB gjennomsnitt, og at det dessuten har noe høyere crest factor i diskanten enn i bassen. Dette er
ikke et loudness war-produkt.
Den røde kurven er ørets høreterskel ved ulike frekvenser ihht ISO226. Dette var tidligere kjent som Fletcher-Munson-kurven eller Equal Loudness Contour, men er nå en ISO standard for normal hørsel. Den strekker seg fra 20 Hz til 20 kHz, når pr definisjon 0 dB ved 1 kHz, og er mest følsom mellom 3 og 4 kHz.
De gule rektanglene er det som kan representeres på et digitalt opptak. Den lyse er 16 bits med 44,1 kHz samplefrekvens. Som kjent rekker det opp til 22,05 kHz. Den oppmerksomme vil igjen legge merke til at det går ned til -141,5 dB, ikke de mer kjente -96 dB. Denne grafen representerer støytettheten fra 16 bits ved en gitt frekvens når kvantiseringsstøyen spres jevnt utover 20 kHz båndbredde. En enkelt tone med all signalenergi i den ene tonen vil såvidt stikke opp av dette støygulvet ved -141 dB signalnivå. De kjente 96 dB SNR fremkommer som integralet av denne støytettheten over båndbredden. Eller 98,08 dB SNR hvis man strekker det til Nyquist-frekvensen ved 22,05 kHz og regner mer nøyaktig. Det mørkere rektangelet er tilsvarende, men med 24 bits og 192 kHz sample rate.
Så langt kan vi kanskje være enige om at det skal være et underlig lydsignal for å være hørbart (over den røde kurven) men
ikke målbart på moderne 24-bits måleutstyr (dvs ikke inni det mørkegule rektangelet).
Men vi tenker oss et mer plausibelt, men litt overforenklet signal: En ren sinus ved A = 440 Hz, 85 dB SPL. Dette signalet er markert med et kors på grafen nedenfor. En realistisk musikalsk tone vil også ha en rik overtonestruktur, men nå er vi interessert i om forvrengningskomponenter kan tenkes å bli hørbare, og da er det enklere å se dem isolert. Dette overforenkler litt, siden vi implisitt ser bort fra intermodulasjonsforvrengning mellom de enkelte harmoniske komponentene av signalet.
Vi antar også at dette signalet går gjennom en dings med 0,25 % THD, men med vekt på lavereordens forvrengningskomponenter. Andreordens er høyest, ned 55 dB fra signalet (dvs ca 35 dB SPL), og deretter fallende med 10 dB pr orden. Disse forvrengningskomponentene er vist som "halen" av blå kors som faller bratt nedover ca midt på grafen. 0,25 % THD kan f eks representere en bra høyttaler. Elektromekaniske transducere som høyttalere og pickuper domineres gjerne av lavereordens forvrengning på denne måten, siden det er mekaniske masser, demping og fjæring i sving.
Men det skjer også noe i øret. Grunntonen ved 440 Hz maskerer for andre toner som ligger nær i frekvens og lavere i nivå. De overdøves. Jeg har skissert inn konturen av maskeringen i brunt på grafen. Toner under den brune kurven er ikke hørbare, selv om de ligger over den røde høreterskelen. De er maskert av grunntonen ved 85 dB.
Poenget her er at alle forvrengningskomponenter ligger innenfor maskeringen eller under høreterskelen i dette (konstruerte) eksempelet. Ja, det er 0,25 % THD der, mediokre -52 dB, men det er
ingen hørbar forvrengning. Whatsoever. (Men husk overforenklingen med at vi utelater overtonestrukturen fra den musikalske tonen og derfor også intermodulasjonsforvrengningen. Den kan fortsatt gjøre mye stygt her, men ikke på et så enkelt signal som dette.)
Denne dingsen måler slett ikke dårlig, vel å merke hvis den er en høyttaler.
Hvis vi i stedet kjører signalet gjennom en dings med "bare" 0,02 % THD, litt mer anstendige -74 dB, kan det se ut som nedenfor. Grunntonen og maskeringen er fortsatt den samme, men jeg har antatt et forvrengningsspektrum med vekt på oddeordens og som har høyest nivå ved sjuende- og niendeharmoniske. Dette kan representere en R2R DAC på en dårlig dag, eller en gammel transistorforsterker "med moderat bruk av global feedback".
Forvrengningskomponenter treffer nå midt i ørets mest følsomme område, de ligger utenfor maskeringen og over høreterskelen, og vil formodentlig være lett hørbare som en "hardhet" eller lignende. Om dette var en DAC eller forsterker koblet til høyttaleren i forrige eksempel ville det fortsatt være lett å høre ulyden fra elektronikken (0,02 % THD) gjennom denne høyttaleren (0,25 % THD).
Skjønn det! som min gamle historielærer pleide å si.
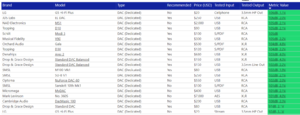
Men for nok en gang å svare på spørsmålet fra åpningsinnlegget: Ja, det har jo skjedd en hel del med elektronikk de siste 30 årene eller så. En noenlunde velkonstruert DAC av i dag ligger på 110 dB SINAD (0,0002 % THD+N) eller deromkring, gjerne begrenset av støy heller enn forvrengning. En Topping E30 ($129,99!) har alle forvrengningskomponenter lavere enn -120 dB fra signalet. Det kan for eksempel se slik ut, 0,0003 % THD (-110 dB):
Lykke til med å høre det der. Det gjør ikke all verdens praktisk forskjell om serien starter på -121 dB eller -126 dB, om den faller med 6 eller 10 dB pr orden, eller om den er mest likeordens eller oddeordens. Det vil ikke være mulig å høre noen som helst forskjell, selv om det fortsatt er eminent målbart. Alle tilstrekkelig gode DAC'er låter klin likt.
Sånn, da kan dere fortsette diskusjonen.