- Ble medlem
- 17.05.2010
- Innlegg
- 196
- Antall liker
- 3
Hei godtfolk!
Tenkte å prøve å få gitt en relativt liten innføring i diffusere og deres bruksområde. Blir nødvendigvis kortere enn det som trengs for det fulle overblikket. Ekstremt kort fortalt er en diffuser et objekt basert på et spesifikt mattestykke. Det som ser ut som en tilfeldig rekke med ulike dybder er tilfeldighet satt i nitidig system. For de som ikke orker å lese noe mer så er kjappeste løsningen å gå til http://www.subwoofer-builder.com/qrdude.htm - last ned kalkulatoren og følg forslagene den gir. For de som vil vite litt mer....:
Med begrepet "akustisk diffuser" menes vanligvis et objekt som sprer lyd både i tid og frekvens. Nedenfor vises absorbasjon, refleksjon og diffusjon som funksjon både av tidsspredning(temporal response) og fysisk spredning(spatial response):

(specular reflection vil si speilrefleksjon)
I praksis vil spredningen i tid si at klangen gir mindre interferens (comb filtering) om det er en tidlig refleksjon, ellers så gir diffusjonen opplevelsen av rikere og fyldigere klang om det er snakk om sene refleksjoner.
Når refleksjonene fra veggene kommer, i forhold til direktelyden fra høytaleren, har alt å si for hvordan lyden oppleves. Tidlige refleksjoner smelter sammen med direktelyden og gir informasjon om rommets størrelse/egenskaper. Eller, sett på en annen måte, smørje i frekvensresponsen! Senere refleksjoner blir oppfattet som en distinkt enhet, "romklang", som ikke påvirker opplevd frekvensrespons direkte. Begrepet romklang er bl.a. definert som at det er statistisk like sannsynlig at lyden kommer fra alle retninger. Slike tilstander finnes bare i meget store rom, type konsertsaler. I små rom blir det aldri tett nok med refleksjoner til at det blir proper romklang, det blir bare en serie med adskilte refleksjoner. Dette er bl.a. en av årsakene til at små rom har problemer med å bli kvitt lyden av å være et lite rom. Det er først og fremst i denne sammenheng diffusere har så mye for seg! Ved å spre ekkoene utover i tid og rom vil øret få en opplevelse av klang som kommer fra mange ulike retninger, spredd godt utover i tid.
Nedenfor vises tids-respons grafer av et rom før/etter akustisk behandling:

(fra denne utmerkede artikkelen: http://www.rpginc.com/news/library/TechBullDiffCritList.pdf )
Tidlige refleksjoner har i grafen nederst blitt dempet nok til å skape en Reflection Free Zone. Legg merke til at det er område i tid som er "fritt" for refleksjoner, ikke et fysisk område uten refleksjoner overhodet. Et slikt rom vil oppleves som nøytralt men samtidig livlig, uten den unaturlige lyden av å dempe alt for mye. Er mange årsaker til at det fungerer dårlig å overdempe et rom. Kort fortalt liker de aller fleste å ha en rik og fyldig romklang, så lenge det ikke skaper interferens med direktelyden! Diffusernes spredning i tid gir en rikere og fyldigere klang som minner mer om responsen som finnes i større rom/konsertsaler.
Det var en del om hva diffusere brukes til. Det var ikke det posten skulle handle om, egentlig.
Diffusere skiller seg markant fra andre konstruksjoner ved at de er tungt basert på matte. Kravet for å få spredd lyden jevnt utover i rommet er at objektet har en tilfeldig overflate. Det høres kanskje lett ut å lage et tilfeldig objekt. Å kaste en terning mange nok ganger vil gi en tilfeldig rekke med tall. Problemet er at det forutsetter at terningen kastes opp mot uendelig mange ganger! Å lage en relativt kort rekke med tall som er "tilfeldig" er et eget kapitell i vitenskapen. Hva er så tilfeldig? Støy er et godt eksempel på tilfeldig. Hvit støy er definert som like mye energi i alle frekvensbånd. Ikke tilfeldigvis fungerer det utmerket å definere diffusere på samme måten. Problemet er at praktiske utførelser av diffusere må være begrenset til en relativt kort tallrekke. Da trengs det meget spesifike regnestykker for å få laget en sekvens som har egenskapen at det gir jevn spredning i alle frekvensbånd (som igjen tilsvarer jevn spredning i alle fysiske retninger).
Den originale ideen ble unnfanget av Manfred Schroeder på 70-tallet. Første forsøkene ble gjort med diffusere med kun to ulike nivåer, slik som denne:

Forsøkene ble gjort med radiofrekvente signaler og ga gode resultater. Problemet var at de kun fungerte på 1 frekvens.
Senere kom Schroeder på en enda bedre idé, å bruke såkalte Quadratic Residues for å lage Diffuserne. Disse gir spredning over et større frekvensregister. Det er den mest utbredte typen diffuser i dag, mye fordi han ikke ville ta patent men heller ville dele oppfinnelsen med verden(stor takk til Manfred(RIP) for det!). Quadratic Residue Diffusere (QRD's) ser typisk slik ut:

Alle slike er basert på primtall. Forklaringen finnes i krypteringens verden. Diffuseren over er basert på tallet 7 og sekvensen er 0-1-4-2-2-4-1. Som det vises er slike QRD'er symmetriske objekter. Diffusjonen foregår på tvers av stripene, lyd som treffer på langs av stripene blir ikke spredd nevneverdig. Ligger en haug med info og en genialt fet kalkulator for slike diffusere på: http://www.subwoofer-builder.com/qrd.htm og http://www.subwoofer-builder.com/qrdude.htm - kalkualtoren gir også varsel om vanlige feller som er lett å gå i.
På de matematiske riktige frekvensene vil objektet sende ut en rekke stråler, med samme antall stråler som primtallet sekvensen er basert på. Her vises samme type diffuser i Falstads ripple tank simulator:

Forskjellen på den vanlige refleksjonen til høyre og den diffuse refleksjonen til venstre bør være tydelig! ("lydkilden" er i midten på toppen) Her er samme forskjellen animert: http://vimeo.com/6461707
Denne animasjonen viser responsen på ulike frekvenser: http://vimeo.com/7507997 - legg merke til at lave frekvenser ikke blir diffusert.
Diffuserne er konstruert slik at de gir den matematisk beregnede responsen på en grunnfrekvens og hele multiplikasjoner av grunnfrekvensen. F.eks har en typisk diffuser noe sånt som 600Hz grunnfrekvens, fulgt av teoretisk korrekt respons på 1200Hz, 1800Hz, 2400Hz osv opp til øvre grensefrekvens. Øvre grense er satt av bredden på hver stripe i diffuseren. Med f.eks. 3,4 centimeter bredde blir øvre grense (343/0,034)/2=~5000Hz (der 343 (meter/sekund) er sånn ca lydhastighet i luft). Baksiden ved å bruke tynnere striper er at absorberingen blir større. Diffusere sprer lyd, men de spiser også noe energi. Først og fremst ved friksjon mot overflatene. Jo tynnere og dypere stripene er, jo mer overflate er det på objektene og jo mer energi forsvinner. Normal grunnregel er å unngå striper som tynnere enn 2,5 centimeter på 25cm dybde.
Dybden på diffuseren setter nedre grensefrekvens. Det er summen av alle hullene som utgjør responsen til diffuseren. Det medfører at nedre grenseverdi ikke er direkte koblet til den fysiske størrelsen og lydhastigheten, slik øvre grense er. I 0-1-4-2-2-4-1 sekvensen basert på primtallet 7 er høyeste tallet som er i bruk 4. Diffuseren jobber ned til "7", mens fysisk dybde bare er 4. Gevinsten i frekvensrespons er 7/4=1,75. Om diffuseren er f.eks. 34cm dyp vil fysiske grensen være (343/0,34)/2=~500 Hz, mens faktisk grunnfrekvens vil være 500*0,57=285Hz. Slike diffusere får dermed en ganske stor gevinst i nedre frekvensrespons. Til gjengjeld er primtallet lavt, som medfører en begrenset spredning av lyden og begrenset spredning utover i tid. Sekvensen har jo bare 4 ulike dybder, så det blir ikke så himla komplisert respons.
En annen måte å lage diffusere på er ved å bruke krypteringsalgoritme basert på "primite root". Slike Primitive Root Diffusere er på en del vis mer avansert enn QRD diffuserne. Bl.a. bruker QRD'ene bare halvparten av tallene mellom 1 og primtall minus 1, mens PRD'ene bruker alle tallene. Hver enkelt stripe i diffuseren får sin egen unike dybde. En annen bonus er at energien som går i retningen av speilrefleksjonen blir noe dempet. Ikke fullstendig dempet, så det fungerer ikke å bruke en slik diffuser til å fjerne speilrefleksjon, men det er likevel en interessant egenskap. Til gjengjeld er det aldri noen spesiel bonus å hente i nedre grunnfrekvens, da slike diffusere alltid bruker samtlige tall mellom 1 og primtall minus 1. Tredje appleten på denne siden (quadratic residues with a primite root) kalkulerer PRD talrekke for ethvert primtall: http://www.math.mtu.edu/mathlab/COURSES/holt/dnt/quadratic4.html Begge disse diffuserne er 1D, de sprer lyd i 1 plan.
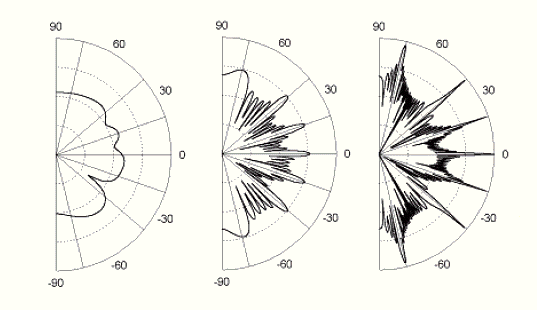
2D diffusere kan lages både av QRD's og PRD's. Disse sprer lyd både langs horisontal og vertikal akse. Responsen fra en slik diffuser kan se slik ut:

(fra http://www.rpginc.com/research/r001c.htm)
Fordelen er en overlegen spredning av lyd, både i område og i tid. Baksiden er at det kan være negativt å spre lyden for mye. Om det f.eks. er ønskelig å holde lyden i det horisontale planet (typisk på høyde med lytteren) kan det være bedre å bruke 1D diffusere.
I praksis kan 2D QRD diffusere slik ut:

Mens 2D PRD diffusere kan se slik ut:

Som det kan sees er QRD'ene symmetriske objekter med et meget spesifikt mønster. Mens PRD'ene karaktiseres ved det totale fraværet av mønster. I min bok gir PRD overlegen respons, i hvert fall for 2D diffusere. Men det kan selvsagt diskuteres! Kalkulator for 2D PRD diffusere ligger her: http://www.oliverprime.com/prd.php - kravet for å bruke kalkulatoren er at man finner et primtall der primtall minus 1 kan settes opp i et rutemønster der hver akse er såkalt "co-prime". F.eks. er 13*12=156, 13 og 12 har ingenting felles utenom seg selv og 1 (er coprime) og 157 er et primtall. Det går opp. 6*7 er også "coprimes" og 43 er et primtall, så det går opp. Her er en liste over primtall (med primite root) som gir nær firkantet oppsett. "Primitive roots" kan også finnes i den andre appleten i den før nevnte lenken her.
Diffusere basert på slike mattestykker er laget for å ha skillevegger mellom lommene. Uten skillevegger gir de ikke den matematiske beregnede responsen, men om objektet er komplisert nok fra før, som med 2D diffuserne, spiler det liten rolle. Det gir fortsatt svært gode diffusive egenskaper, som bekreftet gjennom en rekke målinger. Fordelen med å droppe skilleveggene er lavere absorbering. Baksiden er muligheten for at det gir dårligere spredning om ikke objektet er komplisert nok. Er alltids for og bakdeler med alt!
En annen viktig ting å ha i bakhodet er at diffuserne bare gir matematisk korrekt respons på noen frekvenser, men de sprer lyd i bøtter og spann også mellom, over og under disse frekvensene. Forutsetningen er at diffuseren i seg selv er stor nok. Når bølgelengden til lyden blir større en diffuseren vil lyden brette seg rundt objektet. Så en dyp nok, men ikke bred nok diffuser, vil ikke kunne gjøre noe med dype frekvenser. F.eks. er det vanlig å lage 60cm brede akustikkobjekter (siden 2 fot er vanlig mål i byggeverden) og disse kan ikke gjøre noe med lyd under (343/0.6)=571Hz.
For de som har lyst å fordype seg finnes det 1 bok; Acoustic Absorbers and Diffusers av Cox og D'Antonio. Den ene boken er Bibelen for feltet og mer enn verdt pengene for de som ønsker å vite hva som virkelig foregår.
Så.. Det var i alle fall en begynnelse. Regner med det gir noen svar og noen spørsmål. Fyr løs med spørsmål der det trengs, så vokser tråden etter behov!
Med vennlig hilsen,
Andreas Nordenstam
Tenkte å prøve å få gitt en relativt liten innføring i diffusere og deres bruksområde. Blir nødvendigvis kortere enn det som trengs for det fulle overblikket. Ekstremt kort fortalt er en diffuser et objekt basert på et spesifikt mattestykke. Det som ser ut som en tilfeldig rekke med ulike dybder er tilfeldighet satt i nitidig system. For de som ikke orker å lese noe mer så er kjappeste løsningen å gå til http://www.subwoofer-builder.com/qrdude.htm - last ned kalkulatoren og følg forslagene den gir. For de som vil vite litt mer....:
Med begrepet "akustisk diffuser" menes vanligvis et objekt som sprer lyd både i tid og frekvens. Nedenfor vises absorbasjon, refleksjon og diffusjon som funksjon både av tidsspredning(temporal response) og fysisk spredning(spatial response):

(specular reflection vil si speilrefleksjon)
I praksis vil spredningen i tid si at klangen gir mindre interferens (comb filtering) om det er en tidlig refleksjon, ellers så gir diffusjonen opplevelsen av rikere og fyldigere klang om det er snakk om sene refleksjoner.
Når refleksjonene fra veggene kommer, i forhold til direktelyden fra høytaleren, har alt å si for hvordan lyden oppleves. Tidlige refleksjoner smelter sammen med direktelyden og gir informasjon om rommets størrelse/egenskaper. Eller, sett på en annen måte, smørje i frekvensresponsen! Senere refleksjoner blir oppfattet som en distinkt enhet, "romklang", som ikke påvirker opplevd frekvensrespons direkte. Begrepet romklang er bl.a. definert som at det er statistisk like sannsynlig at lyden kommer fra alle retninger. Slike tilstander finnes bare i meget store rom, type konsertsaler. I små rom blir det aldri tett nok med refleksjoner til at det blir proper romklang, det blir bare en serie med adskilte refleksjoner. Dette er bl.a. en av årsakene til at små rom har problemer med å bli kvitt lyden av å være et lite rom. Det er først og fremst i denne sammenheng diffusere har så mye for seg! Ved å spre ekkoene utover i tid og rom vil øret få en opplevelse av klang som kommer fra mange ulike retninger, spredd godt utover i tid.
Nedenfor vises tids-respons grafer av et rom før/etter akustisk behandling:

(fra denne utmerkede artikkelen: http://www.rpginc.com/news/library/TechBullDiffCritList.pdf )
Tidlige refleksjoner har i grafen nederst blitt dempet nok til å skape en Reflection Free Zone. Legg merke til at det er område i tid som er "fritt" for refleksjoner, ikke et fysisk område uten refleksjoner overhodet. Et slikt rom vil oppleves som nøytralt men samtidig livlig, uten den unaturlige lyden av å dempe alt for mye. Er mange årsaker til at det fungerer dårlig å overdempe et rom. Kort fortalt liker de aller fleste å ha en rik og fyldig romklang, så lenge det ikke skaper interferens med direktelyden! Diffusernes spredning i tid gir en rikere og fyldigere klang som minner mer om responsen som finnes i større rom/konsertsaler.
Det var en del om hva diffusere brukes til. Det var ikke det posten skulle handle om, egentlig.
Diffusere skiller seg markant fra andre konstruksjoner ved at de er tungt basert på matte. Kravet for å få spredd lyden jevnt utover i rommet er at objektet har en tilfeldig overflate. Det høres kanskje lett ut å lage et tilfeldig objekt. Å kaste en terning mange nok ganger vil gi en tilfeldig rekke med tall. Problemet er at det forutsetter at terningen kastes opp mot uendelig mange ganger! Å lage en relativt kort rekke med tall som er "tilfeldig" er et eget kapitell i vitenskapen. Hva er så tilfeldig? Støy er et godt eksempel på tilfeldig. Hvit støy er definert som like mye energi i alle frekvensbånd. Ikke tilfeldigvis fungerer det utmerket å definere diffusere på samme måten. Problemet er at praktiske utførelser av diffusere må være begrenset til en relativt kort tallrekke. Da trengs det meget spesifike regnestykker for å få laget en sekvens som har egenskapen at det gir jevn spredning i alle frekvensbånd (som igjen tilsvarer jevn spredning i alle fysiske retninger).
Den originale ideen ble unnfanget av Manfred Schroeder på 70-tallet. Første forsøkene ble gjort med diffusere med kun to ulike nivåer, slik som denne:

Forsøkene ble gjort med radiofrekvente signaler og ga gode resultater. Problemet var at de kun fungerte på 1 frekvens.
Senere kom Schroeder på en enda bedre idé, å bruke såkalte Quadratic Residues for å lage Diffuserne. Disse gir spredning over et større frekvensregister. Det er den mest utbredte typen diffuser i dag, mye fordi han ikke ville ta patent men heller ville dele oppfinnelsen med verden(stor takk til Manfred(RIP) for det!). Quadratic Residue Diffusere (QRD's) ser typisk slik ut:

Alle slike er basert på primtall. Forklaringen finnes i krypteringens verden. Diffuseren over er basert på tallet 7 og sekvensen er 0-1-4-2-2-4-1. Som det vises er slike QRD'er symmetriske objekter. Diffusjonen foregår på tvers av stripene, lyd som treffer på langs av stripene blir ikke spredd nevneverdig. Ligger en haug med info og en genialt fet kalkulator for slike diffusere på: http://www.subwoofer-builder.com/qrd.htm og http://www.subwoofer-builder.com/qrdude.htm - kalkualtoren gir også varsel om vanlige feller som er lett å gå i.
På de matematiske riktige frekvensene vil objektet sende ut en rekke stråler, med samme antall stråler som primtallet sekvensen er basert på. Her vises samme type diffuser i Falstads ripple tank simulator:

Forskjellen på den vanlige refleksjonen til høyre og den diffuse refleksjonen til venstre bør være tydelig! ("lydkilden" er i midten på toppen) Her er samme forskjellen animert: http://vimeo.com/6461707
Denne animasjonen viser responsen på ulike frekvenser: http://vimeo.com/7507997 - legg merke til at lave frekvenser ikke blir diffusert.
Diffuserne er konstruert slik at de gir den matematisk beregnede responsen på en grunnfrekvens og hele multiplikasjoner av grunnfrekvensen. F.eks har en typisk diffuser noe sånt som 600Hz grunnfrekvens, fulgt av teoretisk korrekt respons på 1200Hz, 1800Hz, 2400Hz osv opp til øvre grensefrekvens. Øvre grense er satt av bredden på hver stripe i diffuseren. Med f.eks. 3,4 centimeter bredde blir øvre grense (343/0,034)/2=~5000Hz (der 343 (meter/sekund) er sånn ca lydhastighet i luft). Baksiden ved å bruke tynnere striper er at absorberingen blir større. Diffusere sprer lyd, men de spiser også noe energi. Først og fremst ved friksjon mot overflatene. Jo tynnere og dypere stripene er, jo mer overflate er det på objektene og jo mer energi forsvinner. Normal grunnregel er å unngå striper som tynnere enn 2,5 centimeter på 25cm dybde.
Dybden på diffuseren setter nedre grensefrekvens. Det er summen av alle hullene som utgjør responsen til diffuseren. Det medfører at nedre grenseverdi ikke er direkte koblet til den fysiske størrelsen og lydhastigheten, slik øvre grense er. I 0-1-4-2-2-4-1 sekvensen basert på primtallet 7 er høyeste tallet som er i bruk 4. Diffuseren jobber ned til "7", mens fysisk dybde bare er 4. Gevinsten i frekvensrespons er 7/4=1,75. Om diffuseren er f.eks. 34cm dyp vil fysiske grensen være (343/0,34)/2=~500 Hz, mens faktisk grunnfrekvens vil være 500*0,57=285Hz. Slike diffusere får dermed en ganske stor gevinst i nedre frekvensrespons. Til gjengjeld er primtallet lavt, som medfører en begrenset spredning av lyden og begrenset spredning utover i tid. Sekvensen har jo bare 4 ulike dybder, så det blir ikke så himla komplisert respons.
En annen måte å lage diffusere på er ved å bruke krypteringsalgoritme basert på "primite root". Slike Primitive Root Diffusere er på en del vis mer avansert enn QRD diffuserne. Bl.a. bruker QRD'ene bare halvparten av tallene mellom 1 og primtall minus 1, mens PRD'ene bruker alle tallene. Hver enkelt stripe i diffuseren får sin egen unike dybde. En annen bonus er at energien som går i retningen av speilrefleksjonen blir noe dempet. Ikke fullstendig dempet, så det fungerer ikke å bruke en slik diffuser til å fjerne speilrefleksjon, men det er likevel en interessant egenskap. Til gjengjeld er det aldri noen spesiel bonus å hente i nedre grunnfrekvens, da slike diffusere alltid bruker samtlige tall mellom 1 og primtall minus 1. Tredje appleten på denne siden (quadratic residues with a primite root) kalkulerer PRD talrekke for ethvert primtall: http://www.math.mtu.edu/mathlab/COURSES/holt/dnt/quadratic4.html Begge disse diffuserne er 1D, de sprer lyd i 1 plan.
2D diffusere kan lages både av QRD's og PRD's. Disse sprer lyd både langs horisontal og vertikal akse. Responsen fra en slik diffuser kan se slik ut:

(fra http://www.rpginc.com/research/r001c.htm)
Fordelen er en overlegen spredning av lyd, både i område og i tid. Baksiden er at det kan være negativt å spre lyden for mye. Om det f.eks. er ønskelig å holde lyden i det horisontale planet (typisk på høyde med lytteren) kan det være bedre å bruke 1D diffusere.
I praksis kan 2D QRD diffusere slik ut:

Mens 2D PRD diffusere kan se slik ut:
Som det kan sees er QRD'ene symmetriske objekter med et meget spesifikt mønster. Mens PRD'ene karaktiseres ved det totale fraværet av mønster. I min bok gir PRD overlegen respons, i hvert fall for 2D diffusere. Men det kan selvsagt diskuteres! Kalkulator for 2D PRD diffusere ligger her: http://www.oliverprime.com/prd.php - kravet for å bruke kalkulatoren er at man finner et primtall der primtall minus 1 kan settes opp i et rutemønster der hver akse er såkalt "co-prime". F.eks. er 13*12=156, 13 og 12 har ingenting felles utenom seg selv og 1 (er coprime) og 157 er et primtall. Det går opp. 6*7 er også "coprimes" og 43 er et primtall, så det går opp. Her er en liste over primtall (med primite root) som gir nær firkantet oppsett. "Primitive roots" kan også finnes i den andre appleten i den før nevnte lenken her.
Diffusere basert på slike mattestykker er laget for å ha skillevegger mellom lommene. Uten skillevegger gir de ikke den matematiske beregnede responsen, men om objektet er komplisert nok fra før, som med 2D diffuserne, spiler det liten rolle. Det gir fortsatt svært gode diffusive egenskaper, som bekreftet gjennom en rekke målinger. Fordelen med å droppe skilleveggene er lavere absorbering. Baksiden er muligheten for at det gir dårligere spredning om ikke objektet er komplisert nok. Er alltids for og bakdeler med alt!
En annen viktig ting å ha i bakhodet er at diffuserne bare gir matematisk korrekt respons på noen frekvenser, men de sprer lyd i bøtter og spann også mellom, over og under disse frekvensene. Forutsetningen er at diffuseren i seg selv er stor nok. Når bølgelengden til lyden blir større en diffuseren vil lyden brette seg rundt objektet. Så en dyp nok, men ikke bred nok diffuser, vil ikke kunne gjøre noe med dype frekvenser. F.eks. er det vanlig å lage 60cm brede akustikkobjekter (siden 2 fot er vanlig mål i byggeverden) og disse kan ikke gjøre noe med lyd under (343/0.6)=571Hz.
For de som har lyst å fordype seg finnes det 1 bok; Acoustic Absorbers and Diffusers av Cox og D'Antonio. Den ene boken er Bibelen for feltet og mer enn verdt pengene for de som ønsker å vite hva som virkelig foregår.
Så.. Det var i alle fall en begynnelse. Regner med det gir noen svar og noen spørsmål. Fyr løs med spørsmål der det trengs, så vokser tråden etter behov!
Med vennlig hilsen,
Andreas Nordenstam