Men her forutsetter man lik strøm i alle ledere når man sier 9 uH gjør man ikke? Metoden for partiell induktans forutsetter nettopp lik strøm i alle lederne og kan ikke brukes. Det blir en systematisk feil på grunn av for enkle formler.Her er det lavest impedans i det innerste paret, men samtidig er det 35 andre lederpar i parallell som også er "open for business". Frekvensen er den samme for alle ledere, så ved høye frekvenser vil en leder med 9 uH fortsatt få 1/3 av strømmen som går i en leder med 3 uH. Det hele ser ut til å gjennomgå en slags faseovergang fra DC (hvor resistansen bestemmer strømfordelingen) til høyfrekvent AC (hvor induktansen regjerer). Det omslaget skjer midt i audiobåndet. Når den overgangen er fullført skjer det ikke så mye mer.
Minste impedans - en fortsettele
- Trådstarter Hedde
- Startdato
Diskusjonstråd Se tråd i gallerivisning
-
Dette er riktig og jeg viste tall lengre oppe. (4,5 uH for en enkelt leder til 3,8 uF for to ledere med strøm samme vei). Men man må huske på at da øker middellengden til retur fra 2 mm til over 4 mm.Derimot ser jeg kommentarer i lærebøkene og formelsamlingene av typen "the inductance will be reduced when the current is divided among several conductors", så jeg kan ikke utelukke at dette er riktig.
Nei, som jeg allerede har forklart to-tre ganger, så regnet jeg ut gjensidige induktanser mellom alle kombinasjoner av ledere vektet med den strømmen som går i hver enkelt av dem, med behørig hensyn til både retning og størrelse. Selve formelen for gjensidig induktans sier ingen ting om størrelsen på strømmen, men det tok jeg hensyn til når jeg summerte de gjensidige induktansene for å få den partielle induktansen for hver enkelt leder. Da ble hvert enkelt bidrag vektet med den andelen av strømmen som gikk i den aktuelle lederen. Derfra fikk jeg et nytt sett med partielle induktanser, som gjorde at jeg kunne regne ut nye strømmer, and repeat. Første iterasjon startet med en antagelse om lik fordeling av strømmen, men så handlet resten stort sett om å regne ut hvordan den egentlig ville fordele seg.Men her forutsetter man lik strøm i alle ledere når man sier 9 uH gjør man ikke? Metoden for partiell induktans forutsetter nettopp lik strøm i alle lederne og kan ikke brukes. Det blir en systematisk feil på grunn av for enkle formler.
Det regnestykket tror jeg er nokså riktig, men jeg skal se en gang til på hvordan jeg summerte de resultatene til induktans for hele kabelen. Den var et litt kjapt tillegg på slutten, og der er jeg ikke like sikker.Sist redigert:
Den setningen som er uthevet skjønte jeg ikke. Kan du forklare hvordan du regnet?Selvinduktansen for en enkelt leder, 2,5 meter er 4,5 uH. Det blir 9 uH med retur som ligger utenfor magnetfeltet (langt unna). Men det blir 2,2 uH når retur er svært nær.
Ser man på selvinduktansen for to ledere i samme polaritet med 1 mm luft mellom seg, blir dette L=3,8 uH, eller 7,6 uH med retur langt borte. Med forutsetning om lik strøm i begge lederne blir nå induktansen for hele greia, når retur også består av to ledere med 1 mm luft mellom seg, 2,7 uH. Om man korrigerer for ulik strømfordeling, så nærmer man seg igjen 2,2 uH når all strøm går innerst.
Jeg ser ikke hvordan man skulle kunne få noen geometriske varianter av dette som har L=1,5 uH, uten å ha to enkeltledere liggende 1 mm inntil hverandre, med strøm i hver sin retning.
Jeg mener at proximity effekten er nettopp grunnet minste impedans. Man kunne tenke seg at man delte lederen inn i skiver og regnet på den som enkeltledere, med hver sin partiell induktans. Man skulle kunne bruke samme metode som her.
Lik strøm i begge ledere betyr at jeg kan regne som om at strømmen i sin helhet går midt mellom dem. Altså gir denne forutsetningen avstanden mellom effektiv tur og effektiv retur.Den setningen som er uthevet skjønte jeg ikke. Kan du forklare hvordan du regnet?
Om man ser på siste avsnitt på første side i appendikset om partiell induktans, om to parallelle ledere med strøm i samme retning, så ser man at dette betinger lik strøm i begge ledere, eller sagt på en annen måte, stor avstand til returleder. Den vektingen av andelen av strømmen som går i hver leder for å regne et ett nytt sett med partielle induktanser, er kanskje tvilsom når man også bruker formelen i nevnte avsnitt i appendikset. For den formelen umuliggjør jo at det bare går strøm i en leder. Når det går strøm bare innerst, så skulle alle andre L være meget stor.
Nei, som jeg allerede har forklart to-tre ganger, så regnet jeg ut gjensidige induktanser mellom alle kombinasjoner av ledere vektet med den strømmen som går i hver enkelt av dem, med behørig hensyn til både retning og størrelse. Selve formelen for gjensidig induktans sier ingen ting om størrelsen på strømmen, men det tok jeg hensyn til når jeg summerte de gjensidige induktansene for å få den partielle induktansen for hver enkelt leder. Da ble hvert enkelt bidrag vektet med den andelen av strømmen som gikk i den aktuelle lederen. Derfra fikk jeg et nytt sett med partielle induktanser, som gjorde at jeg kunne regne ut nye strømmer, and repeat. Første iterasjon startet med en antagelse om lik fordeling av strømmen, men så handlet resten stort sett om å regne ut hvordan den egentlig ville fordele seg.Men her forutsetter man lik strøm i alle ledere når man sier 9 uH gjør man ikke? Metoden for partiell induktans forutsetter nettopp lik strøm i alle lederne og kan ikke brukes. Det blir en systematisk feil på grunn av for enkle formler.
Det regnestykket tror jeg er nokså riktig, men jeg skal se en gang til på hvordan jeg summerte de resultatene til induktans for hele kabelen. Den var et litt kjapt tillegg på slutten, og der er jeg ikke like sikker.
Når man kommer med slike forutsetninger som s>>d, eller lik strøm i lederne etc, så er det gjerne fordi man i utledningen av formlene har brukt nettopp slike størrelser til å fjerne hele ledd i formlene. Jeg tror vi må tilbake til mere komplette formler om skal skal komme i mål med forståelsen. Men jeg tror også at svaret mitt for noen uker siden ikke var så veldig galt. Metoden var i bunn og grunn å bruke middelavstander basert på en antatt strømfordeling som gav minste impedans. Middelavstander kan man bruke på mange slike avstandsavhengige krefter.Link: http://www.ursi.org/proceedings/procGA11/ursi/E07-9.pdf
Jeg fant en bra artikkel om viktigheten av å ta hensyn til proximity effekten ved lavspente kraftkabler. Disse kablene har den egenskapen at lederavstand er i samme størrelsesorden som lederdiameteren. Som de skriver i konklusjonen: "Denne effekten er bare relevant for frekvenser i kHz området og høyere".
Kurvene vist i fig 3 i artikkelen viser at den interne motstanden øker ved relativt lave frekvenser, mens intern induktans faller. Dette i en massiv leder!!!
Dette indikerer at de to fenomenene oppfører seg likt, og sannsynligvis har samme årsak, virvelstrømmer som motsetter seg feltet. De lederne i flatkabelen som ikke fører strøm i langsretningen fører virvelstrømmer i aksielle retninger som motsetter seg feltet og fører til at loopen kun omkranser de innerste delene ved høy frekvens.
Artikkelen bruker FEM (element-metode beregninger som løser originale Maxwell ligninger med grensebetingelser), men sammenligner også dette med en metode de kaller Schelkunoff.
Her er det vell bare FEM beregninger eller målinger på selve flatkabelen som til slutt kan verifisere forløpet.Sist redigert:Jeg skal gjøre et forsøk til ved anledning, men jeg har jo følelsen av å skyte etter spurv med kanon her, hvis vi ser mengde jobb vs betydning for lydkvaliteten. Netto forskjell mellom de tallene vi diskuterer er hvorvidt den induktive toppen i frekvensgang ved 8-10 kHz blir ca 0,1 eller ca 0,2 dB høy. Å sette opp en detaljert FEM-modell for å regne ut dette er noe i retning av å skyte etter spurven med atomtuppede mellomdistansemissiler. Derimot koster et bra LCR-meter bare et par tusenlapper på Elfa, så det er jo en tanke.
Ellers har du rett i at proximity-effekten i en massiv leder kan modelleres som et stort antall "filaments", og det blir også gjort.Tallene viser jo at induktansen vil bli ett mindre "problem" når proximity eller "minste impedans" spiller en rolle.
Men jeg har ikke helt fått en god forståelse for hva 400% høyere resistans gjør ved 10 kHz. Eller hva denne generelle økningen i resistansen i audioområdet gjør. Det nevnes jo stadig at den eneste virkelig viktige parameter for høyttalerkabler er tverrsnitt. Beregningene mine i innlegg #114 viser jo at strømmen vil gå utelukkende i innerste leder ved 20 kHz. Det er en reduksjon på 1800% i resistans i forhold til ved under 1 kHz. Dette kan vell ikke være uten betydning.
Om dette er av betydning, så kan jeg gjerne regne ut med høyere oppløsning selv for å få bedre og mere nøyaktige tall mellom 1 kHz og 20 kHz. Jeg er bare styrket i troen på at disse tallene er i rett ballpark etter jeg regnet på de.Sist redigert:Jeg fant feilen. Beregningen av partielle induktanser og strømfordeling ser fortsatt riktig ut, men jeg hadde glemt å ta med de gjensidige induktansene når jeg summerte til en enkelt induktansverdi per meter. Jeg hadde brukt L = L1 + L2 for seriekobling og 1/L = 1/L1 + 1/L2 for parallell, men de formlene skal egentlig være L = L1 + L2 - 2 L12 og L = (L1L2 - L122)/(L1 + L2 - 2 L12). Den summeringen jeg brukte gjelder bare med stor avstand mellom lederne, og det er ikke tilfelle her. Det forklarer nok hvorfor den samlede induktansverdien ble altfor lav, men det er ikke helt trivielt å utvide de formlene til 72 enkeltledere. Skal gjøre et forsøk - manaña.
De gjensidige induktansene i seg selv er en rent geometrisk størrelse. Jeg grov meg tilbake i lærebøkene, og det ligger ingen antagelse om likt fordelte strømmer der. De gjensidige induktansene er et uttrykk for hvor stor spenning som vil bli indusert i en bestemt leder hvis strømmen i en annen leder endrer seg, uansett hvor store eller små strømmer det var i utgangspunktet. Det kommer bare an på avstanden mellom lederne og formen på hver leder. Det er først når de gjensidige induktansene skal summeres til en partiell induktans for hver enkelt leder at man må ta hensyn til strømretning og -størrelse, hvis de altså ikke er like. Og det gjør jeg. Derfor mener jeg fortsatt at de regnestykkene og grafene er riktige.
For det første blir det ikke slik. Strømfordelingen blir slik som grafene mine viser. Ja, det går mer strøm i innerste lederpar ved 20 kHz enn ved 1 kHz, men det er bare en faktor på 2 sammenlignet med lederparet med minst strøm. Det er ingen ledere som "slås av" fullstendig. Alle leder hele tiden, både ved 20 kHz og 20 MHz, selv om strømmen ikke lenger er helt likt fordelt mellom lederne.Tallene viser jo at induktansen vil bli ett mindre "problem" når proximity eller "minste impedans" spiller en rolle.
Men jeg har ikke helt fått en god forståelse for hva 400% høyere resistans gjør ved 10 kHz. Eller hva denne generelle økningen i resistansen i audioområdet gjør. Det nevnes jo stadig at den eneste virkelig viktige parameter for høyttalerkabler er tverrsnitt. Beregningene mine i innlegg #114 viser jo at strømmen vil gå utelukkende i innerste leder ved 20 kHz. Det er en reduksjon på 1800% i resistans i forhold til ved under 1 kHz. Dette kan vell ikke være uten betydning.
Om dette er av betydning, så kan jeg gjerne regne ut med høyere oppløsning selv for å få bedre og mere nøyaktige tall mellom 1 kHz og 20 kHz. Jeg er bare styrket i troen på at disse tallene er i rett ballpark etter jeg regnet på de.
For det andre har det minimal betydning. Den induktive reaktansen tar over for resistansen. Husk at impedansen er |Z| = kvadratrot( R2 + X2 ), og at X = 2 p f L. Ved 20 kHz er den induktive reaktansen 20000 ganger større enn ved 1 Hz, hvis vi ser bort fra de forholdsvis små frekvensavhengige endringene av L. Det disse regnestykkene viser er at den induktive reaktansen tar over kontrollen et sted rundt 5 kHz, og at den overgangen er ettertrykkelig fullført ved 10 kHz. Da har R ikke lenger noe å si.
Litt tilfeldig valgte tall: R = 1,0 milliohm og L = 5 uH ved 1 Hz. Da er reaktansen X = 2 p 1 5e-6 = 0,314 uOhm. Impedansen er Z = kvadratrot( 1e-3^2 + 3,1e-5^2 ) = 1,0 milliohm. Men ved 20 kHz blir reaktansen X = 2 p 20000 5e-6 = 0,63 ohm, og impedansen blir Z = kvadratrot ( 1e-3^2 + 0,63^2 ) = 0,63 ohm. Om resistansen firedobles til 0,004 ohm er det fortsatt mindre enn avrundingsfeilen i den utregningen. Ved 20 khz er resistansen parkert og det er induktansen som regjerer.Sist redigert:Vi ser ut til å nærme oss i det minste ;-)
Er du fortsatt av den formening at "minste impedans" og proximity effekten er to ulike ting?
Hvordan kan man forklare at resistansen i en massiv leder endrer seg 600% når frekvensen øker mye?Jeg har aldri fått helt tak på hva du mener med "minste impedans". Strømmen vil fordele seg mellom alle tilgjengelige veier, med en fordeling som er omvendt proporsjonal med impedansen i hver vei. Proximity-effekten handler om hvordan virvelstrømmer inne i en metallisk leder tvinger strømmen ut til overflaten på siden nærmest en leder med motsatt strømretning. Den kan modelleres og beregnes ved metoder som de vi leker med her, men egentlig er det noe annet.
Første overslagsberegning, basert på avstanden mellom tyngdepunktet for strømmen i hver retning ved respektive frekvens. Vi later som at all strømmen går i et mikroskopisk tynt filament der. Det er det du kalte "middelavstand" for noen innlegg siden, her kalt D:
1 Hz: D = 19,94 mm, L = 1,98 uH per meter
1000 Hz: D = 19,70 mm, L = 1,97 uH pr meter
10000 Hz: D = 18,24 mm, L = 1,94 uH pr meter
20000 Hz: D = 18,10 mm, L = 1,94 uH per meter.
Dette blir 4,95 uH - 4,85 uH for 2,5 meter og 0,60 - 0,59 uH per fot.
Til sammenligning: Ytter- og innerkantene i midtskillene mellom de to ledergruppene i hver retning ligger hhv 20 og 18 mm fra hverandre. Tyngdepunktet flytter seg tilsvarende bredden på den stripen. Den første utregningen min, hvor kablene ble representert som 18 mm brede foliestrimler plassert 2 mm fra hverandre, ga en induktans på 1,40 uH per meter. Hvis vi i stedet antar at hele ledertverrsnittet er plassert som runde ledere med disse middelavstandene får vi noe lavere tall i størrelsesorden 1,20 - 1,16 uH per meter.
Da er vi ihvertfall i samme "ballpark" som de forenklede regnestykkene med flate og runde ledere. Og vi er fortsatt skyhøyt over de verdiene Nordost selv oppgir, men de tallene har vi uansett aldri trodd på.Sist redigert:Proximity og skinneffekten er begge drevet av "minste impedans".
At any given frequency, alternating currents take the path of least impedance. Currents tend to accumulate at the outer layer or skin of conductors since magnetic fields of the device penetrate the conductors and produce opposing electric fields within the volume of conductors.
En kilde (s.23) : http://rfic.eecs.berkeley.edu/~niknejad/pdf/NiknejadPhD.pdf
Her forklarer man altså at skinneffekten oppstår på grunn av "minste impedans" og at det settes opp virvelstrømmer inni selve lederen som motsetter seg /motvirker feltet som oppstår på grunn av strømmen i lederen. Resultatet er altså virvelstrømmer inni lederen, mindre effektivt tverrsnitt for strømmen i lederen og mindre selvinduktans.
Tilsvarende for proximity effekten i massive ledere. Det vil settes opp virvelstrømmer på en side av lederen, som motsetter seg feltet. Strømmen blir sviset mellom feltene fra virvelstrømmen og den nærliggende lederen. Resultatet er altså virvelstrømmer på en side av lederen, mindre effektivt tverrsnitt for strømmen i lederen og mindre induktans (mindre loop).
Tilsvarende for flatkabel med mange ledere. Det settes opp virvellstrømmer i lederene som ligger lengst bort. Det skapes et felt som motsetter seg påvirkningen, og strømmen i langsretningen "slås av". Resultatet er altså virvelstrømmer inni lederne som ligger lengst bort, mindre effektivt tverrsnitt for strømmen i lederne og mindre induktans (mindre loop).
Siden magnetfeltet fra returlederen er så svakt på de lederne som ligger lengst bort, og så sterkt på de lederne som ligger helt inntil retur, så blir "minste impedans" synlig ved så lave frekvenser som i audioområdet mens de andre to variantene først er synlige ved svært høye frekvenser. Kraftkabler hvor avstanden mellom lederne er i samme størrelsesorden som lederdiameteren vil også ha synlig proximity effekt ved lave frekvenser.Sist redigert:Grunnen til at jeg misliker begrepet "minste impedans" eller tilsvarende utsagn som at "strømmen går minste motstands vei" er at det gjør den ikke. Den går alle veier, med en fordeling som er omvendt proporsjonal med impedansen i hver enkelt vei. Det er ingen veier som "slås av", selv om andre veier har mindre impedans.
For meg holder det med at induktansen setter opp en spenningsforskjell over en leder proporsjonalt med endringen i strømmen i andre ledere. Det er hva induktans gjør, pr definisjon. Det vi regner på her er hvordan alle de lederne påvirker hverandre ved audiofrekvenser. Virvelstrømmer/eddy currents/skin effect/proximity effect hører hjemme i et annet frekvensområde enn hva vi regner på her.Nei, jeg linket tidligere i dag til ett underlag som tydelig sa at proximity effekten startet ved 1 kHz i det aktuelle tilfellet med en kraftkabel. De sirkulerende virvelstrømmene har også induktans og setter derfor opp ett eget magnetfelt for å utligne det påtrykte feltet.
Eddy current - Wikipedia, the free encyclopediaSkinneffekten gjør også at ledninger tykkere enn en centimeter eller så er bortkastet metall allerede ved 50 Hz. Det er et poeng hvis du skal overføre noen megawatt i en kraftlinje, men fortsatt lite relevant for de ledertykkelsene og frekvensene vi holder på med i audio.
Ved enda mye høyere frekvenser vil skinneffekten trekke strømmen ut mot overflaten i hver leder, og proximity-effekten vil trekke strømmen i det innerste lederparet inn mot kanten nærmest strøm i motsatt retning. Utover i båndet vil proximity-effekten presse strømmen mot over- og undersiden av båndet, siden den prøver å "komme seg unna" strøm i samme retning. Det ytterste lederparet vil påvirkes i mye mindre grad av proximity-effekter enn det innerste, fordi det befinner seg lengre unna strømmen som går i motsatt retning og har tre fjerdedeler av omkretsen i fri luft. Husk at styrken på magnetfeltene faller med kvadratet av avstanden. Netto effekt blir at strømmen i innerste lederpar vil se litt større motstand enn i ytterste ved MHz-frekvenser. Dette skrur ikke av strømmen i ytterste par, men drar littegranne i motsatt retning.
I prinsippet kunne vi tatt med alt det også i modellen ved å representere de enkelte lederne som et antall "filamenter" med ulike plasseringer i tverrsnittet av hver leder. Da måtte vi først gjort modellen to-dimensjonal, siden hvert filament må plasseres i X- og Y-retning, ikke bare sidelengs som vi har gjort hittil. Deretter måtte vi utvide alle matriser og regnestykker til å håndtere ~1500 filamenter i stedet for 72. Så kunne vi sett hvor høy frekvensen må bli før det blir noen vesentlig forskjell mellom de enkelte filamentene innenfor tverrsnittet av hver enkeltleder. Det ville blitt en riktigere modell, siden jeg så langt har representert hver enkelt leder som et tynt filament heller enn en leder med en fysisk utstrekning, men det blir også en vesentlig mer kompleks modell med minimal økning i nytteverdi.
Jeg tror dette er omtrent så langt som vi kommer. Du har tydeligvis bestemt deg for at strømmen skal oppføre seg på en bestemt måte, og da hjelper det nok ikke om jeg lager stadig mer detaljerte regnestykker som viser noe annet. Så langt er oppsummeringen for min del at dette er en reell effekt, at ca 5-6 % av strømmen går i innerste lederpar ved frekvenser øverst i audiobåndet, at det er ca dobbelt så mye som i lederne midt i det ytterste båndet, at induktansen i kabelen faller ørlittegranne med økende frekvens, og at Nordost juger med de tekniske spesifikasjonene på produktene sine.Sist redigert:Link: http://www.ursi.org/proceedings/procGA11/ursi/E07-9.pdf
Jeg må igjen vise til at en av mine kilder (link ovenfor) viste, på en tydelig måte, at proximity effekten viste seg allerede ved 1kHz og at den påvirket en massiv leder, ca 600% ved høye frekvenser. Det som er av betydning for ved hvilke frekvenser dette spiller inn, er som du korrekt sier, avstand mellom lederne og diameteren på selve lederen. På det siste ser det ikke ut til at vi er uenige. Men uenigheten går på om proximity effekten er den som forklarer flatkabelen, og om ytterpunktet for denne mekanismen gir liten effekt eller stor effekt (flere hundre prosent høyere resistans).
Her er noen tilfeller satt opp i en figur.
a) viser konfigurasjonen som gav 600% økning i resistansen ved svært høye frekvenser*. Drivkraften er her forskjellen i avstand mellom de punkter på lederne som ligger nærmest og de som ligger lengst borte, eller egentlig midt i kabelen. Variasjonen er her 0,8 - 1 (4*d til 5*d).
b) viser forholdet når avstanden er d. Variasjonen er her 0,5 - 1 (d til 2*d). Forholdet var også omtalt i artikkelen jeg linket til.
c) viser forholdet når avstanden er 0,2*d. Variasjonen er her ca 0,2 - 1 (0,2*d til 1,2*d). Denne konfigurasjonen vil helt klart påvirkes sterkt av priximityeffekten.
d) viser forholdet for en flat kabel når avstanden er 0,2*d. Variasjonen er her ca 0,2 - 1 (0,2*d til 1,2*d). Altså samme drivkraft som i c).
Skulle ikke proximity effekten på en flat kabel som ligger slik som i d), gi mye større proximity effekt enn tilfellet i a) ?
At den så består av ett antall "slicer" spiller ingen rolle egentlig. Jeg har tegnet opp ett sideblikk på loopen som bestemmer induktansen i tilfellet ved lave frekvenser (sort) og høye frekvenser (rød).
Når man henviser til at proximity effekten kun spiller inn ved svært høye frekvenser, så gjør man det på grunn av de relative dimensjonene. Har man to tynne ledere som ligger i behørig avstand, kanskje på grunn at isolasjonetykkelsen, så er dette korrekt. Om man har to ledere som ligger helt inntil hverandre, og som har områder som ligger vesentlig lengre borte fra hverandre, så spiller proximity effekten helt klart en rolle innenfor audiobåndet. Dette er ingenting jeg har funnet på, det bare er sånn.
Så når man sier at dette kun drar littegranne i motsatt retning ved MHz frekvenser så har vi svært ulik oppfatning. Noen sier 600%, noen sier 6%!!
Det hjelper ikke at du lager mere og mere detaljerte regnestykker når de ikke er korrekte. Det vises jo klart og tydelig når frekvensen blir veldig høy. Da oppfører ikke regnestykket seg som det skal. Dette ser man jo fort, og da kan man heller ikke feste lit til svaret ved lavere frekvenser.
Men jeg tror heller ikke at vi kommer særlig mye lengre i dette. Og for den aktuelle casen var det egentlig ikke så veldig spennende. Den kabelen låter jo ikke bra.
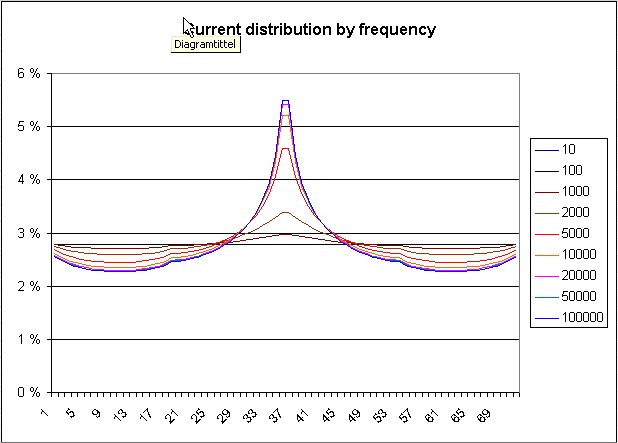
*Edit: Jeg gjorde en ks og fant at tilfellet som gav 600% større resistans var når avstanden i mellom lederne var 4 ganger lederradius og ikke 4 ganger lederdiameteren. Rett skal være rett.Sist redigert:Jeg mener nok fortsatt at den strømfordelingen jeg regnet ut er riktig. Den viser effekten av gjensidige induktanser for frekvenser gjennom audiobåndet. Slik blir det, med frekvenser som øker fra 10 Hz til 100 kHz:

Den fordelingen er beregnet fra "første prinsipper" og tar med hvordan strømmene i de forskjellige lederne påvirker hverandre gjennom gjensidig induktans. Det brukes til å beregne impedans for hver leder. Deretter beregnes hvordan strømmen vil fordele seg mellom forskjellige veier med litt forskjellig impedans. Så gjentas hele den prosessen inntil induktanser og strømmer er konsistente.
Det som ikke er med her er utstrekningen av hver enkelt leder og skinn- og proximity-effekter innenfor hver enkelt leder. I prinsippet kan det gjøre en liten forskjell hvis lederne er såpass tykke at den forflytningen av strømmen innenfor hver enkelt leder gjør en forskjell for magnetfeltet rundt andre ledere, altså at ledertykkelsen er stor sammenlignet med avstanden mellom lederne og frekvensene så høye at det skjer en betydelig overføring av strøm til overflaten på hver leder.
Disse lederne er tvert i mot seriøst tynne sammenlignet med de 18 mm avstand fra innerste til ytterste leder på hver side. Om proximity-effekten fører til at all strømmen i den innerste lederen flytter seg til innerkanten, så gjør det minimal forskjell for den effektive avstanden mellom den strømmen og den ytterste lederen. Skinn- og proximity-effekter i hver enkelt leder påvirker nesten ikke avstandene mellom strømmene. I den innerste lederen dras strømmen litt innover og i den ytterste skyves den litt utover, men det er med brøkdeler av en lederdiameter.
De fleste lederne ligger hverken innerst eller ytterst, men inne mellom andre ledere med strøm i samme retning. For disse presses strømmen hovedsakelig oppover og nedover til overflatene av kabelen heller enn sidelengs. Det gjør enda mindre forskjell for den effektive avstanden mellom de strømmene og andre ledere.
Disse effektene vil slå inn ved riktig høye frekvenser. En pekepinn er at skinndybden i kobber er ca 0,5 mm ved 20 kHz, så i de tynne lederne i den aktuelle kabelen vil hele tverrsnittet fortsatt lede strøm ved 20 kHz. Det betyr at skinn- og proximity-effekter fortsatt har minimal påvirkning ved den frekvensen, og da er vi allerede ute av audiobåndet. Derfor mener jeg at den grafen ovenfor har fått med alle vesentlige effekter til et eller annet sted godt over audiobåndet.
Alle linkene dine forklarer at skinn- og proximity-effekter er noe som foregår inne i massive ledere, forresten. Grunnen til det er at de skyldes virvelstrømmer, eddy currents, som sirkulerer inne i den ene lederen. Første setninger fra Wikipedia-artikkelen om proximity effect, min utheving:
Det jeg bommet på i første forsøk var å summere alle de partielle induktansene til en aggregert induktansverdi for hele kabelen. Det regnestykket var mer komplisert enn jeg innså først, men tilnærmingen med en effektiv middelavstand bør komme ganske nær. Ligningene er lineære, slik at det i prinsippet er mulig å regne ut eksakt riktig svar på den måten. Regnestykket gir plausible resultater sammenlignet med beregninger for folieledere og runde enkeltledere med tilsvarende avstand. Det kan enkelt verifiseres med en måling på den virkelige kabelen ved ulike frekvenser.In a conductor carrying alternating current, if currents are flowing through one or more other nearby conductors, such as within a closely wound coil of wire, the distribution of current within the first conductor will be constrained to smaller regions. The resulting current crowding is termed the proximity effect.
Og fortsatt er det ganske uviktig om resistansen skulle øke med 600 % fra 10 Hz til 20 kHz, hvis den induktive reaktansen øker med 200000 % samtidig. Da er det til slutt den som bestemmer impedansen, og den eventuelle økningen i resistans forsvinner nedenfor avrundingsfeilene.Sist redigert:
Jeg tror også det er riktig, men så var det dette med den minste impedansen da. Du har 6% ved høye frekvenser. Jeg har 600% men skal være med på at det er 606% for å være litt humoristisk alvorlig.Jeg mener nok fortsatt at den strømfordelingen jeg regnet ut er riktig. Den viser effekten av gjensidige induktanser for frekvenser gjennom audiobåndet. Slik blir det, med frekvenser som øker fra 10 Hz til 100 kHz:
Jeg er helt enig i at man kan se bort fra proximity effekter inni en enkelt nordostleder. Den vil ikke ha en geometrisk utstrekning av betydning. Det har kabelen som en enhet, selv om den består av enkeltledere. Dette sees best om man tenker på den som en folie eller plate. Men la det nå ligge.Alle linkene dine forklarer at skinn- og proximity-effekter er noe som foregår inne i massive ledere, forresten. Grunnen til det er at de skyldes virvelstrømmer, eddy currents, som sirkulerer inne i den ene lederen.
Da slutter vi denne debatten med dette utsagnet om at flere hundre prosent økning i resistansen ikke har noenting å si for lyden i en kabel. Det er helt greit. Debatten har til tider vært lærerik og det er faktisk hovedsaken. Takk for det!Og fortsatt er det ganske uviktig om resistansen skulle øke med 600 % fra 10 Hz til 20 kHz, hvis den induktive reaktansen øker med 200000 % samtidig. Da er det til slutt den som bestemmer impedansen, og den eventuelle økningen i resistans forsvinner nedenfor avrundingsfeilene.Sist redigert:- Ble medlem
- 04.03.2004
- Innlegg
- 8.699
- Antall liker
- 7.007
Takk for interessant diskusjon alle tre!Ikke meningen å gjenåpne debatten, men når strømmen i innerste lederpar øker fra 2,78 % av totalen ved 20 Hz til 5,46 % av totalen ved 20 kHz, så er det en økning på 96 % i strømtetthet, ikke 6 % økning. En dobling, rett og slett. Det endrer likevel ikke resistansen i denne modellen av kabelen.
Artikkelen fra ursi.org som det ble linket til ovenfor er interessant. Den ser på tre ledere med 1 mm radius, altså 2 mm diameter og 3,14 mm2 tverrsnitt pr leder, som ligger inntil hverandre. Den radien er ca det dobbelte av skinntykkelsen ved 20 kHz. Avstanden mellom lederne er bare 1 mm isolasjon utenpå hver leder, altså 2 mm mellom lederoverflatene eller 4 mm mellom senterlinjene. Artikkelen viser at proximity-effekter inne i de tre lederne gjør at motstanden i hver leder øker omtrent som kvadratroten av frekvensen, samtidig som induktansen faller. I den modellen øker resistansen i hver enkelt leder med en faktor på ca 5 - 6x fra DC til 20 kHz. Samtidig faller selvinduktansen til ca 1/3 - 1/4 av verdien ved DC.
Den induktive reaktansen øker som X = 2 pi f L, så endringen i induktans vil være vel så viktig ved høye frekvenser som endringen i resistansen. Med de tallene som er vist i artikkelen vil impedansen ved DC være de resistive 0,005 ohm. Hvis vi ser bort fra proximity-effekten vil impedansen ved 20 kHz bli ca 0,01 ohm, altså like store bidrag fra resistans og induktans. Når vi tar med den effekten blir resistansen større mens reaktansen blir lavere. Netto effekt i det eksemplet er at impedansen ved 20 kHz i stedet blir 0,025 ohm og fortsatt stort sett resistiv. Ikke en 600 % økning, men 250 % økning i impedans er da også noe. Hvis dette var en høyttalerkabel ville den fortsatt stå i serie med en høyttaler med kanskje 8 ohm impedans, og da kan man jo diskutere betydningen av forskjellen mellom 8,010 ohm og 8,025 ohm ved 20 kHz.
Den kabelen vi har regnet på har tynnere ledere og høyere induktans, slik at disse tallene blir ikke direkte overførbare. Med ledertykkelser rundt 1 mm vil hele tverrsnittet lede strøm og vi kan nesten se bort fra skinn- og proximity-effekter. Jeg kan moderere meg litt og innrømme at noe sikkert vil endre seg hvis vi tar med dette, men noen 600 % endring blir det ikke, hverken i resistans eller induktans.Sist redigert:Er det prinsipiell forskjell på en 1 cm folieleder og en nordost flatkabelledergruppe som også er 1 cm bred?
Om svaret er nei, er det prinsipiell forskjell på en 1 cm folieleder og en 1 cm rundkabel mhp proximity?
Det har gradvis gått opp for meg at det ikke er prinsipielle forskjeller på disse konfigurasjonene med hensyn på induktans, og da ble den nevnte artikkelen svært oppklarende med hensyn på at det jeg forklarer som minste impedans er akkurat det samme som proximityeffekten. Og artikkelen var jo fin siden den gav noen tall på bordet som var i samme gate som jeg forventet.
Men å sammenligne disse prosentene med faktiske ohm i lasten, så ser vi jo hvor veien går, og da blir jo dette bare en akademisk øvelse ;-)
Edit: Det er vanskelig å avslutte helt når man har noe på hjertet, så ha meg unnskyldt. Her kommer en liten sak til:
Dette med virvelstrømmer som oppstår i massive ledere på grunn av nærhet til ett annet magnetfelt som trekker litt ulikt på selve lederens sider (klassisk proximity effekt). Det er min forståelse at disse virvelstrømmene ikke fortrenger langsstrømmen (den langs kabelen) direkte, men at de setter opp ett magnetfelt som motvirker magnetfeltet fra den andre lederen. Virvelstrømmer er også strømmer, og de setter opp magnetfelt og de har følgelig også induktans. Men man måler ikke virvelstrøm på klemmene, så denne induktansen vil heller ikke komme til syne på klemmene. Strømmene vil føre til tap, selvsagt små tap.
Siden det er magnetfeltet fra virvelstrømmene som "presser" langsstrømmen innover mot den andre lederen så er ikke det avgjørende om selve lederen er massiv eller om den består av flere enkeltledere.Sist redigert:Virvelstrømmene må ha et sted å gå. De kan ikke hoppe mellom isolerte ledere. Husk at Litz-tråd med isolerte enkeltledere brukes for å redusere skinneffekt ved høye frekvenser. Skinneffekten er en konsekvens av virvelstrømmene inne i lederen. Derfor er det forskjell mellom en massiv folie og en flatkabel med mange isolerte ledere. Induktans og sløyfeareal henger sammen. Virvelstrømmer inne i en millimetertykk leder har ikke stort sløyfeareal. Eddy current - Wikipedia, the free encyclopediaSist redigert:Dette ble igjen interessant
Du har helt rett i at virvelstrømmene ikke kan gå gjennom isolasjonen mellom de ulike lederne og at loopen til de enkelte virvlene blir vesentlig mindre enn i en folieleder eller en massiv leder. Og induktans og loopareal henger sammen. Og i formiddagstimene, sittende i en gapahuk, gikk det opp for meg at dette har betydning.
Fortsatt vil virvelstrømmene oppstå på grunn av "minste impedans" for hele den ekvivalente formen på 1 cm bredde. Skinneffekten derimot vil alltid bare være avhengig av radius på selve lederen, og da vil en litz-leder være av meget stor betydning. Men hvilke betydning vil det ha for proximity effekten at lederne er så tynne?
Om vi ser på hvilke induktans man kan forvente å få ved ulike loopareal så tror jeg dette kan sammenlignes med selvinduktansen i en enkelt massiv leder. Selvinduktansen i en enkelt leder på 2,5 meter varierer fra 4,5 uH ved d=0,54 mm, til 3 uH ved d=1 cm. Den går opp til 6,5 uH ved 0,01 mm.
Energien i feltet er E=1/2 L*I*I
Altså vil samme energi sette opp litt mindre virvelstrøm siden induktansen øker noe ved mindre looper. Eller sagt på en annen måte: Energien som kreves blir noe større ved de samme virvelstrømmene fordi de har mindre loop ved tynne ledere.
Konklusjonen min foreløpig vil være at det betyr noe, men ikke vesentlig mye. Men jeg tror ikke jeg er helt ferdigtenkt på akkurat dette ennå. Men nå kaller påskeplikteneSist redigert:
Det er jo de som sverger til en slik grøftekabelArtikkelen fra ursi.org som det ble linket til ovenfor er interessant. Den ser på tre ledere med 1 mm radius, altså 2 mm diameter og 3,14 mm2 tverrsnitt pr leder, som ligger inntil hverandre. Den radien er ca det dobbelte av skinntykkelsen ved 20 kHz. Avstanden mellom lederne er bare 1 mm isolasjon utenpå hver leder, altså 2 mm mellom lederoverflatene eller 4 mm mellom senterlinjene. Artikkelen viser at proximity-effekter inne i de tre lederne gjør at motstanden i hver leder øker omtrent som kvadratroten av frekvensen, samtidig som induktansen faller. I den modellen øker resistansen i hver enkelt leder med en faktor på ca 5 - 6x fra DC til 20 kHz. Samtidig faller selvinduktansen til ca 1/3 - 1/4 av verdien ved DC.Virvelstrømmer kan være svært så nyttige blant annet til å detektere sprekker i ledende overflater eller som bremser. En slik litt modifisert brems er vist i figuren under.
Her kommer en ledende "pendel" inn i ett magnetfelt, og det induseres virvelstrømmer i det ledende godset som motsetter seg bevegelsen inn i magnetfeltet. Virvelstrømmene øker med økende pendelfart, så bremsen vil oppføre seg mykt. Dette prinsippet brukes etter hva jeg forstår på jernbanen og jeg husker det også fra tungindustrien.
På figuren over er pendelen modifisert ved slisser i metallet i pendelen. Dette gjør at virvlene blir mindre og at de delvis kansellerer hverandre. Resultatet blir at bremseeffekten blir mindre som man delvis var inne på i ett tidligere innlegg. Størst bremseeffekt får man uten slisser i metallet.
Figuren over kan delvis brukes på den omtalte Nordostkabelen siden den er bygget med slisser mellom de enkelte lederne. Magnetfeltet vil her være de gjensidige magnetfeltene fra andre strømførende ledere. Om man tenker seg at ytterste leder fylles opp med slike virvlende strømmer som i figuren over, ser man at alle virvlene har lik retning inn mot neste leder. De vil presse likt på strømmen, og resultatet er at de presser strømmen innover mot retur akkurat som om slissene ikke fantes. Dog kan man anta at hele prosessen krever litt mer tilført energi for samme resultat (kanskje litt spekulativt teori her fra min side). Jeg ser også at så snart en leder opplever virvler, så øker resistensen for strømmen i resten av denne lederen, og det fordeles mindre strøm til denne lederen (ohms lov). Det blir vell litt selvforsterkende effekt som bidrar til å slå av lederen før neste leder opplever virvelstrømmer (igjen litt kreativ spekulasjon fra min side).
Det er uklart om virvelstrømmer er negativt for lyden i en kabel men man kan vell trygt anta at det ikke er positivt iallefall. Så er det jo mulig, faktisk enkelt, å lage kabler som ikke opplever slike effekter i audiobåndet iallefall.
Når det gjelder markedsføring av audiokabler, som denne tråden var en spinnoff fra, så registrerer jeg at svært mange fabrikanter hevder å ha løsninger for skinneffekt og noen for proximity effekt men jeg har bare sjekket noen av de mange der ute.
Jeg ville iallefall unngått flatkabel og solidcore grøftekabel. Jeg trenger ingen virvelstrømsbrems på mine kabler.Llarkus
Gjest
Det ser ut som om det er bare en vei ut av proximity-/skineffekt helvetet, og det er rikelig med tverrsnitt, og da menes RIKELIG.
En screenshot fra denne siden. Effects of wire diameter and spacing (Bla litt frem og tilbake i disse sidene. http://www.st-andrews.ac.uk/~www_pa/Scots_Guide/audio/skineffect/page1.html Mye interessant lesning der)
Som vi ser minker tapet i kabelen p.g.a. proximity-/skineffekt med økende tverrsnitt.
Sitat fra Wikipedia om proximity effekt
Cables
"Proximity effect can also occur within electrical cables. For example, if the conductors are a pair of audio speaker wires, their currents have opposite direction, and currents will preferentially flow along the sides of the wires that are facing each other. The AC resistance of the wires will change (slightly) along with the frequency of the audio signal, though for any frequency, the amplitude of the current will still be linearly proportional to the voltage. Some believe that this will potentially introduce distortion and degrade stereo imaging. However, it can be shown that, for reasonable conductor sizes, spacing, and length, this effect has a small impact on audio quality."
Det er akkurat dette jeg gjentatte ganger har prøvd å banke inn i skallene på hfs-medlemmene.
OPP MED TVERRSNITTET PÅ HT-KABLENE
mvh
larkuzSist redigert:Først av alt, det er ikke påvist eller bevist at proximity effekten er hørbar eller fører til vesentlig forringelse av audiosignalet. Denne tråden viser bare at proximity effekten skjer i enkelte kabelgeometrier ved frekvenser i audiobåndet. Så kan jeg jo legge til at jeg selv hører forringelse som jeg knytter opp mot nettopp dette, men det blir litt tynt å bruke som noe bevis.
Du har vell forsåvidt rett i at tap i kabelen minker ved økende tverrsnitt. Proximity effekten vil være en funksjon av lederradius (eller diameter) og avstand mellom de to lederne i pluss og minus. Altså vil proximity effekten oppføre seg likt om en kabel har radius på 1 meter og det er 1 meter mellom kablenes omkrets, og om kabelen har radius på 1 mm og det er 1 mm mellom kablenes omkrets. (skin effekten prater vi ikke om, men den blir også merkbar i audioområdet ved meget store tverrsnitt).
Kabelgeometrier som ikke vil oppleve proximity effekter i audiobåndet kan være:
- Coax
- Liten radius, stor avstand (kanskje når avstand er større enn ca 4*radius)
- Litz (har nettopp liten radius)
- Ulike tvinninger/flettinger (gjerne kombinert med litz)
- Sikkert noen flere
Det er altså flere veier ut av proximity effekt "helvete". Som sagt tidligere. Virvlende strømmer og ditto felt kan ikke være en god ting.
Hvorfor mener du det når resistansen øker med en faktor på 5 eller 6x over audioområdet, mens også induktans og kapasitans endres, i tillegg til at selve feltene endres. Du må gjerne utdype litt.Virvlende strømmer og ditto felt i høyttalerkabler har nok omtrent samme betydning som å helle ut en flaske Imsdal i Nordsjøen for at havet skal bli mindre salt.
Jeg utelukker slett ikke at proximity effekten kan være uten særlig betydning i høyttalerkabler i vanlige oppsett (men tror den har betydning). Da er det litt interessant at det nå tilbys test/utlån av en Beldenkabel som etter mine begreper vil være offer for nettopp denne effekten. Se denne aktuelle tråden som ble startet tidligere i dag: http://www.hifisentralen.no/forumet...-ve-en-billig-og-bra-kabel-belden-5000ue.html (jeg har ikke testen denne kabelen selv).Sist redigert:
Hvis man ser på hva man faktisk hører i lytteposisjon og hvilke avvik som finnes i hele kjeden så kan man vurdere kabler innflytelse på lyden? Selv om resistansen på en f. eks 2 meter lang høyttalerkabel endrer seg med 5x tviler jeg på om det vil være hørbart i en blindtest.
Hvorfor mener du det når resistansen øker med en faktor på 5 eller 6x over audioområdet, mens også induktans og kapasitans endres, i tillegg til at selve feltene endres. Du må gjerne utdype litt.Virvlende strømmer og ditto felt i høyttalerkabler har nok omtrent samme betydning som å helle ut en flaske Imsdal i Nordsjøen for at havet skal bli mindre salt.
Jeg utelukker slett ikke at proximity effekten kan være uten særlig betydning i høyttalerkabler i vanlige oppsett (men tror den har betydning). Da er det litt interessant at det nå tilbys test/utlån av en Beldenkabel som etter mine begreper vil være offer for nettopp denne effekten. Se denne aktuelle tråden som ble startet tidligere i dag: http://www.hifisentralen.no/forumet...-ve-en-billig-og-bra-kabel-belden-5000ue.html (jeg har ikke testen denne kabelen selv).
Strengt tatt kan vel høyttalerkabelen i sen helhet sees på som et RLC ledd hvor Kirchoff gjelder og ved resonansfrekvensen er motstanden kun ohmsk?
Min innvending handler i hovedsak om at jeg betrakter impedansen som irrelevant lav ved alle audiofrekvenser.
Sannhetsvitner på kabler som det er snakk om i tråden du linker til har etter min mening ingen verdi.SSommerand
Gjest
Der er ikke noget nyt i at man mindsker tabet ved at gøre den ohmske modstand mindre.Det ser ut som om det er bare en vei ut av proximity-/skineffekt helvetet, og det er rikelig med tverrsnitt, og da menes RIKELIG.
En screenshot fra denne siden. Effects of wire diameter and spacing (Bla litt frem og tilbake i disse sidene. http://www.st-andrews.ac.uk/~www_pa/Scots_Guide/audio/skineffect/page1.html Mye interessant lesning der)
Vis vedlegget 192346
Som vi ser minker tapet i kabelen p.g.a. proximity-/skineffekt med økende tverrsnitt.
Sitat fra Wikipedia om proximity effekt
Cables
"Proximity effect can also occur within electrical cables. For example, if the conductors are a pair of audio speaker wires, their currents have opposite direction, and currents will preferentially flow along the sides of the wires that are facing each other. The AC resistance of the wires will change (slightly) along with the frequency of the audio signal, though for any frequency, the amplitude of the current will still be linearly proportional to the voltage. Some believe that this will potentially introduce distortion and degrade stereo imaging. However, it can be shown that, for reasonable conductor sizes, spacing, and length, this effect has a small impact on audio quality."
Det er akkurat dette jeg gjentatte ganger har prøvd å banke inn i skallene på hfs-medlemmene.
OPP MED TVERRSNITTET PÅ HT-KABLENE
mvh
larkuz
Men se evt på det næste billede over delay /fasedrej hvad ulempen ved en tyk leder er, fasedrejet og den ohmske modstand varierer i audio-området, jo tykkere tråd jo mere variation, årsag bl.a (skineffekt),
Skal der opnås helt jævn fase og ohmsk modstand i hele audio-området, og det er vil det som det drejer sig om vil jeg mene.
Så er den optimale diameter på tråden ca 0.8 mm, og for at mindske tabet er man så nødt til at benytte litze-tråd for at øge arealet af den totale leder, der kan også med fordel bruges fladvalset leder .
Der er som vanligt ingen gratis lunch, heller ikke her.Sist redigert:SSommerand
Gjest
proximity effekten kan reduceres væsentligt således at den er helt uden betydning ved audio, med afstand, eller sikre at lederene ikke ligger parallelt, for mere info kan evt. søges på hvordan man laver HF spoler.
Hvorfor mener du det når resistansen øker med en faktor på 5 eller 6x over audioområdet, mens også induktans og kapasitans endres, i tillegg til at selve feltene endres. Du må gjerne utdype litt.Virvlende strømmer og ditto felt i høyttalerkabler har nok omtrent samme betydning som å helle ut en flaske Imsdal i Nordsjøen for at havet skal bli mindre salt.
Jeg utelukker slett ikke at proximity effekten kan være uten særlig betydning i høyttalerkabler i vanlige oppsett (men tror den har betydning). Da er det litt interessant at det nå tilbys test/utlån av en Beldenkabel som etter mine begreper vil være offer for nettopp denne effekten. Se denne aktuelle tråden som ble startet tidligere i dag: http://www.hifisentralen.no/forumet...-ve-en-billig-og-bra-kabel-belden-5000ue.html (jeg har ikke testen denne kabelen selv).Sist redigert:
Greit. Asbjørn argumenterer vell noenlunde likt, og konkluderer med det samme. Når jeg ser på de tallene så er det lett å være enig med ham/dere.Hvis man ser på hva man faktisk hører i lytteposisjon og hvilke avvik som finnes i hele kjeden så kan man vurdere kabler innflytelse på lyden? Selv om resistansen på en f. eks 2 meter lang høyttalerkabel endrer seg med 5x tviler jeg på om det vil være hørbart i en blindtest.
Men vill en RCL analyse alltid gi de relevante svarene man søker? Dette kan eksemplifiseres med følgende figur:Strengt tatt kan vel høyttalerkabelen i sen helhet sees på som et RLC ledd hvor Kirchoff gjelder og ved resonansfrekvensen er motstanden kun ohmsk?
Min innvending handler i hovedsak om at jeg betrakter impedansen som irrelevant lav ved alle audiofrekvenser.
Her ser vi de elektriske E-feltene i figur 5, og de magnetiske H-feltene i figur 6, rundt noen kilder (signalledere). Om man skulle analysere disse ved sine R, C og L, så er det iallefall lett å se at de ville ha litt ulike verdier. L ville vell variere med en faktor på noen titalls prosent. Men dette ville altså være helt irrelevant ifølge alle RCL analysene som presenteres her på forumet. Og så lukker man saken..."case closed"... som man sier. Men vent nå litt.....
Hva er det som skjer med de grønne lederne, the victim? Ingen RCL analyse her? Kan noen se at de grønne lederne blir påvirket av den ene kilden og ikke den andre. Dette kalles for EMC, og er faktisk også en funksjon av L. Dette har relevans for nettkabler hvor selve jordlederen er "the victim". Dette har relevans til signalkabler på flere måter, en av dem pga returlederen gjerne er koplet sammen med nevnte jordleder som altså er ett offer for EMC. Dette kan meget vell ha relevans for enkelte høyttalerkabler. Det er nevnt i denne tråden.
Dette bare som ett eksempel, og ikke en "teori" på proximity effektens forringende egenskaper.
Ikke om man har bestemt seg. Selvsagt.Sannhetsvitner på kabler som det er snakk om i tråden du linker til har etter min mening ingen verdi.Sist redigert:Vvredensgnag
Gjest
Spørs om man ikke også bør ta variasjoner i det ytterste Van Allen beltet i betraktning for å forsvare søkte forvrengningsteorier.En høyttalerledning forbinder en kildeimpedans i størrelsesorden 0,01 ohm med en lastimpedans på ca 8 ohm. Anta at signalet er 16 volt. Da vil det gå 16/8 = 2 A strøm. Det tilsvarer 32 W effekt.
Omtrent hvor sterkt må et eksternt elektrisk og magnetisk felt være før det introduserer et avvik på f eks 0,0001 % (-80 dB) i den høyttalerkabelen? Hvor sannsynlig er det at så sterke elektromagnetiske felter finnes i et boligrom? Hvor nær en 16000 V høyspentlinje må du holde høyttalerkabelen før du når de 0,0001 %?
Jeg måtte tilbake for å se hva jeg hadde skrevet, for å bli forstått på en slik måte. Men det var nok du som leste inn at jeg mente dette. Ekstern felt?En høyttalerledning forbinder en kildeimpedans i størrelsesorden 0,01 ohm med en lastimpedans på ca 8 ohm. Anta at signalet er 16 volt. Da vil det gå 16/8 = 2 A strøm. Det tilsvarer 32 W effekt.
Omtrent hvor sterkt må et eksternt elektrisk og magnetisk felt være før det introduserer et avvik på f eks 0,0001 % (-80 dB) i den høyttalerkabelen? Hvor sannsynlig er det at så sterke elektromagnetiske felter finnes i et boligrom? Hvor nær en 16000 V høyspentlinje må du holde høyttalerkabelen før du når de 0,0001 %?
Figuren var ment som ett eksempel på det jeg skrev om nettkabler og signalkabler og dette kan jeg gjerne skrive mye mer om en annen plass. Det er interessante saker. Men i forbindelsen med høyttalerkabler er det nå en kjensgjerning at feltene fra hver av lederne påvirker den/de andre lederne på måter ingen her på forumet tidligere pratet noe om. Proximityeffekten slår inn ved audiofrekvenser. Det betyr at selve feltene endres, og at nye felter fra virvelstrømmer oppstår (emc in action). Feltene har utstrekning og kan illustreres som på figur 6 i ett tidligere innlegg.
Men la nå ikke dette bli stående som at jeg fremsetter noen spesifikk forvrengningsteori om dette. Jeg har jo ikke brukt F-ordet engang (tror jeg). Poenget mitt var tross alt at RLC teorien ikke svarer tilstrekkelig på de nevnte tilfellene og at det er plausibelt at den også kan være utilstrekkelig når det gjelder høyttalerkabel.
Edit: Denne proximity tråden omhandler endringer i induktans, altså L. Jeg er klart over at jeg la ved et bilde som også inneholdt E feltet, men dette er ikke relevant i denne tråden siden det er strøm vi prater om, selv om enkelte hang seg på dette med E felt.Sist redigert:SSommerand
Gjest
Der er jo også denne artikel jeg har refereret til nogen gange, men artiklen er omdiskuteret da man mener at den gode professor lavede en fejl i det eksperiment som skulle bevise hans teori, som i meget korte træk ist gik ud på at i en ikke ideel leder vil de skævheder påvirkningen som opstår i feltet lagres i plastikisoleringen for så at frigives med delay , en slags hukommelses effekt.
Men matematikken har ingen såvidt jeg ved kunne sætte en finger på.
Derudover viser han at en leder med en diameter på 0.8 mm giver den jævneste impedans i audio-området.
The Essex Echo 1995: Electrical Signal Propagation & Cable Theory | Stereophile.com
Også ude fra kommende felter kan give problemer, felterne/støjen kan komme fra elektronikken selv (Klasse D, SMPS) eller som støj fra andre apparater igen mobiltelefoner, SMPS, radio HF generelt, Pc osv , disse problemer kan overføres Via nettet og luft, og her er kun et at gøre at træffe de nødvendige EMC foranstaltninger, eller prøve at bekæmpe ved at holde afstand, eller lade være at bruge de tekniker som giver støj, men det er svært i dag, prøv at måle omkring noget så dagligdags som en sparepærer som evt ikke er helt frisk.Sist redigert:
Hva du mente vet du best selv, men den illustrasjonen viser hvordan energi fra ett lederpar (aggressor) som fører ett signal overføres via induktiv og kapasitiv kobling til et annet lederpar (victim) som fører et annet signal. Det kan f eks skje når 50 Hz brumming smitter over fra strømkabler til et par RCA signalkabler som ligger for nært. Den støyen er ekstern sett fra signalkabelen, siden den ikke har noen sammenheng med det signalet som skal gå i signalkabelen. Det er hva EMC handler om.Jeg måtte tilbake for å se hva jeg hadde skrevet, for å bli forstått på en slik måte. Men det var nok du som leste inn at jeg mente dette. Ekstern felt?
Electromagnetic compatibility - Wikipedia, the free encyclopedia
Energilagringen i magnetfeltet rundt en og mellom flere ledere med samme signal beskrives som induktans (L) og den tilsvarende energilagringen i det elektriske feltet kalles kapasitans (C). De avhenger av geometrien og materialet som omgir lederne. Jeg ser ikke helt hva nytt den "EMC-teorien" tilfører?Sist redigert:
Om man går litt bak Wikipedia som kilde, så finner man fort ut at EMC ingeniører innen audiobransjen prater om EMC som de ytre påvirkninger mens de prater om den interne elektromagnetiske kompatibiliteten med begreper som signalintegritet og lignende. Derfor handler EMC også om returstrømmer og proximity effekter....Det er hva EMC handler om.
Samme kilde som figrene 5 og 6 i noen innlegg over sier f.eks:
Signal Integrity (SI) and Power Integrity (PI) are subsets of EMC engineering, so employing good EMC design techniques from the start of a new project ensures excellent SI and PI.
Igjen..... jeg har jo ikke fremsatt noen EMC teori om høyttalerkabler og har nevnt det flere ganger allerede. Jeg bare påpeker at RLC teorien ikke svarer tilstrekkelig på de nevnte tilfellene for andre kabler og at det er plausibelt at den også kan være utilstrekkelig når det gjelder høyttalerkabel. Det er jo forhold som griper rett inn i signal integriteten, så EMC er relevant etter min mening....Jeg ser ikke helt hva nytt den "EMC-teorien" tilfører?
Så kan jeg jo legge til på slutten ett kort utdrag om hva Wikipedia artikkelen sier om EMC:
"..unintentional generation, propagation and reception of electromagnetic energy"
Altså langt mer enn bare ekstern støy.
Sist redigert: -
Laster inn…
Diskusjonstråd Se tråd i gallerivisning
-
-
Laster inn…