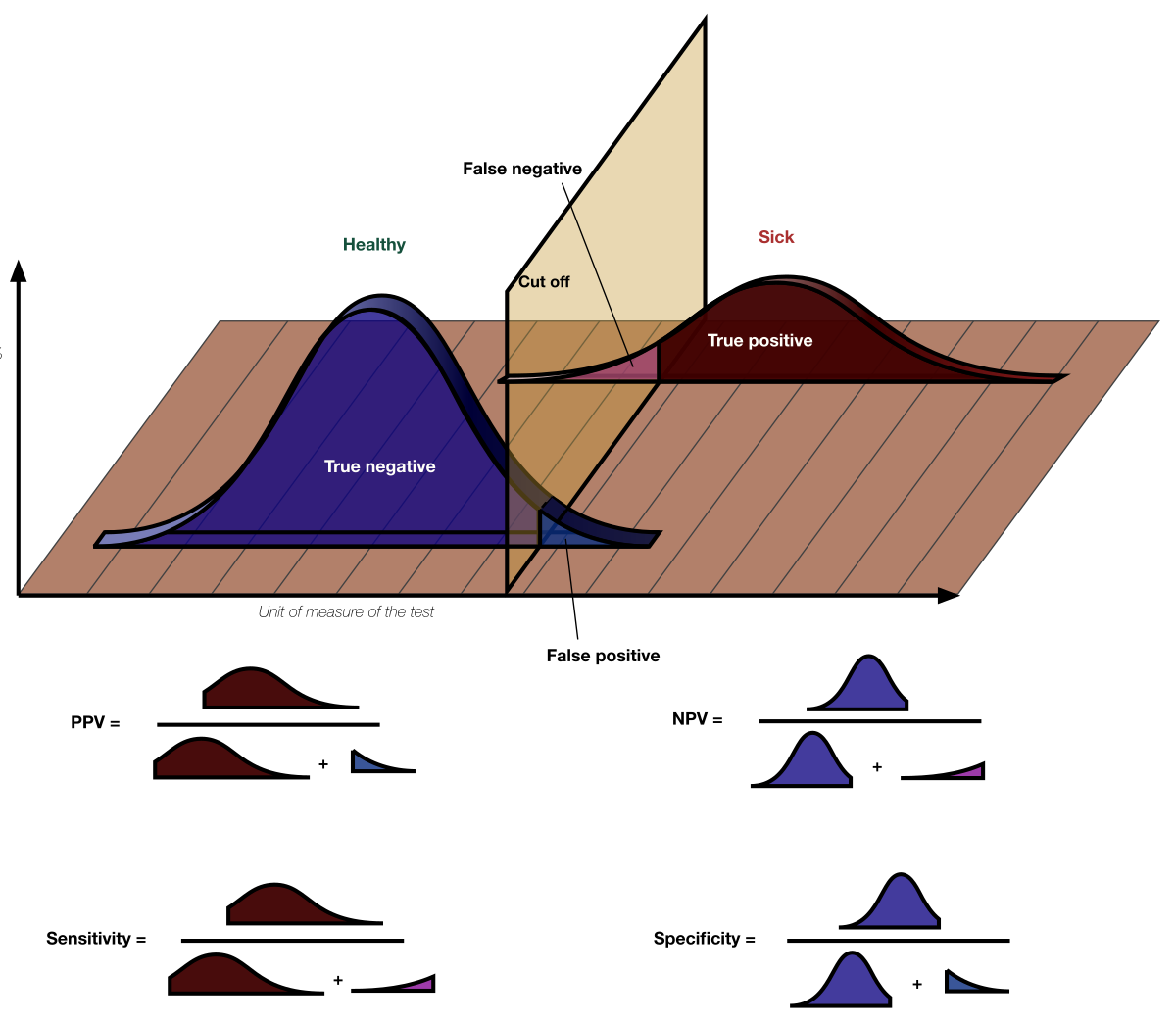
Men det er egentlig stikk motsatt. Enten har en pasient viruset eller ikke. Små mengder virus skal også detekteres. Det vi ønsker svar på er om pasienten har viruset eller ikke.
Testen har en viss sensitivitet og spesifisitet, hhv sannsynlighet for å gi et korrekt
positivt svar hvis pasienten
har viruset, og sannsynlighet for å gi et korrekt
negativt svar hvis pasienten
ikke har viruset.

en.wikipedia.org
Spesifisitet bestemmer også antall falske positive, som 100 % - spesifisitet. Til å begynne med var man litt usikker på hvor gode PCR-testene var, men resultatene fra praktisk bruk viser at de er veldig gode. Når vi ser 99,8-99,9 % negative resultater kan ikke spesifisiteten være dårligere enn det. Da antar vi at
alle positive resultater i den perioden var falske, og det var de nok ikke, men det setter et tak for hvor mange falske positive vi vil få med et visst antall prøver. Mindre enn 0,1-0,2 % av alle prøvesvar.
La oss si at testen har erfaringsbaserte 99,9 % spesifisitet og vil gi 0,1 % falske positive. La oss også si at det er 0,1 % av befolkningen som bærer på viruset, og at vi tester 1000 tilfeldige personer. Da vil vi forvente å ha 1 reell positiv og få 1 falsk positiv, tilsammen 2. Så når vi screener etter et
sjeldent virus vil andelen falske positive bli en høy andel av de positive testresultatene, i dette eksemplet 50 %. Det bør man ta hensyn til når man bruker dette til screening ved lave smittetall, som WHO også påpekte.
Derimot, når vi ser 5, 10 eller 15 % positive resultater vet vi at de 0,1 % falske positive bare er avrundingsfeil og knapt nok det. Det har ingen praktisk betydning om det reelle tallet er 15,0 % eller 14,9 %. Når det er mye virus i omløp gir testen mer presise resultater. Antallet falske positive blir en lav andel av alle positive resultater. Slik det er nå brukes PCR-testen mest til å bekrefte diagnose for noen som har symptomer eller har avlagt en positiv hurtigtest, og man kan rolig gå ut fra at den gir dønn riktig fasitsvar.
Hvis en lege skal bruke den til å diagnostisere en pasient som kommer inn på kontoret med mistenkelige symptomer er den også evig god nok. Hvis legen i utgangspunktet tror det er 50/50 om dette er corona eller forkjølelse er en test med 99,9 % spesifisitet fantastisk bra. Legen er tilnærmet helt sikker på å stille rett diagnose.
Så, hva var feil i Hammarskjolds blogg-post? Mest at han gikk ut fra «tenk på et tall»-metoden og mente at det hadde noe med virkeligheten å gjøre. Da blir konklusjonen hans like frikoblet fra virkeligheten. Deretter later han som om WHOs kommentar om screening ved lave smittetall fortsatt gjelder ved høye. Det stemmer jo ikke. Regnestykket som sådant er forsåvidt riktig. Jeg har selv gjort tilsvarende eksempler her inne med 99 % som utgangspunkt og vist hvordan det vil slå ut. Men heldigvis er det ikke slik de virkelige tallene er.